斯坦福大学机器学习公开课：线性与逻辑回归解析

"这篇笔记详述了斯坦福大学公开课中关于机器学习的前四节内容，主要涵盖了线性回归和逻辑回归的概念以及回归问题在有监督学习中的应用。笔记作者通过对实际问题的引入，展示了如何利用回归方法进行预测，并探讨了学习过程和线性回归模型的构建。" 在机器学习领域，回归是一种基本且重要的有监督学习方法，用于处理连续型数据的预测问题。斯坦福大学公开课中的这部分内容首先提出了回归的基本思想：通过对连续型统计数据建立数学模型，来实现对未知数据的预测或分类。这种方法特别适用于处理具有多个特征的多维数据。 问题的引入通常以实例为起点，比如房屋销售价格的例子，其中训练集包含了房屋面积和对应售价的数据。为了预测新的房屋价格，可以尝试找到一条最佳拟合曲线，例如直线，来尽可能贴近所有已知数据点。在这个例子中，训练数据被标记为x（房屋面积）和y（售价），而模型函数h(x)则表示根据输入x预测的售价。 机器学习的学习过程通常包括以下步骤：给定输入数据，算法通过一系列计算得到一个模型，这个模型能对未见过的新数据进行预测。在本课中，这一过程具体表现为线性回归。 线性回归假设特征和目标变量之间存在线性关系，即y = h(x) = wx + b，其中w是权重参数，b是偏置项。线性回归的目标是找到一组最佳的w和b，使得模型对训练数据的预测误差最小。这通常通过最小化损失函数（如均方误差）来实现，最常见的是梯度下降法或正规方程解法。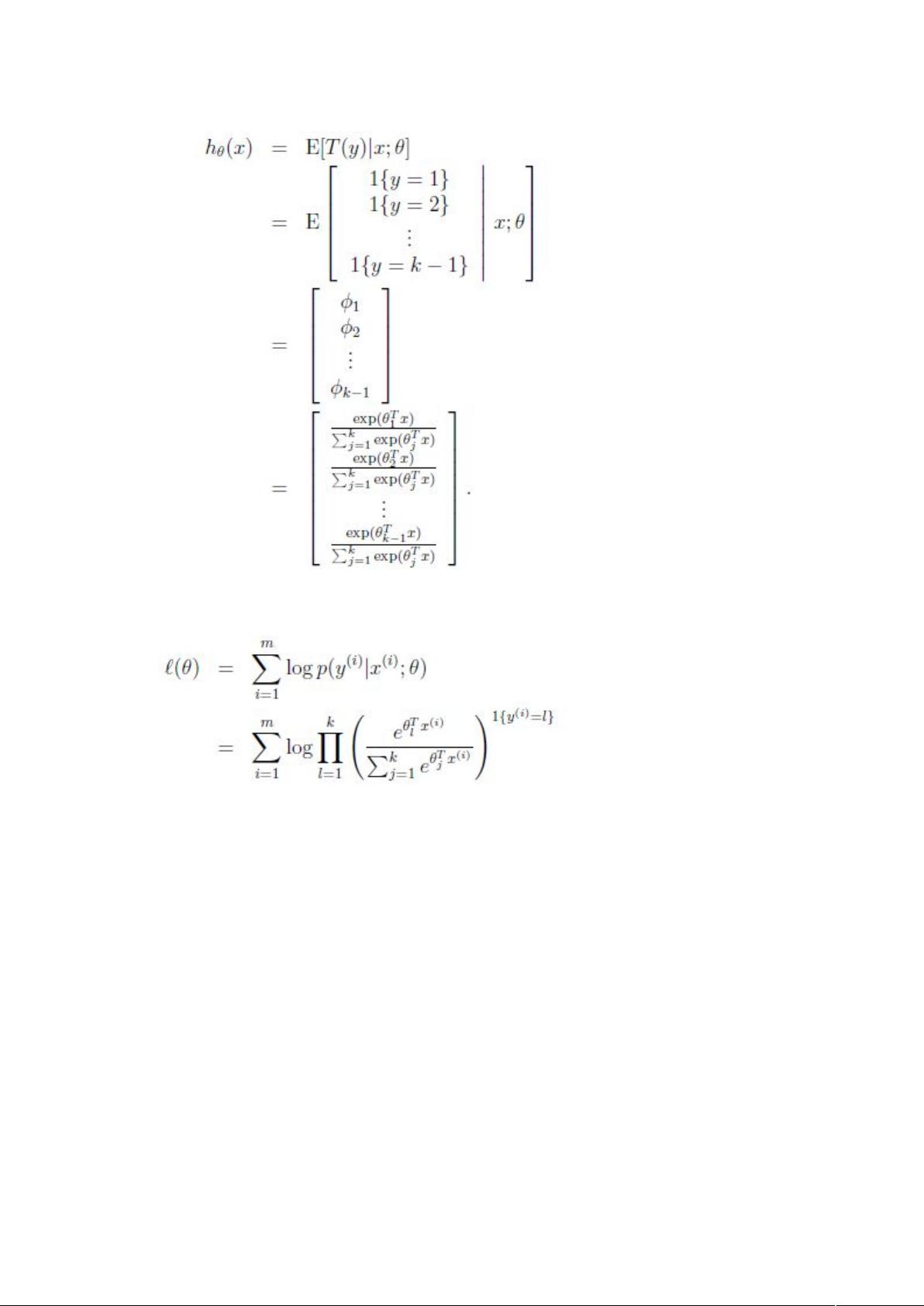 除了线性回归，笔记中还提到了逻辑回归（Logistic Regression）。尽管名字中含有“回归”，但实际上，逻辑回归是一种广泛应用于二分类问题的模型，它通过sigmoid函数将线性组合转换为0到1之间的概率值。 这部分机器学习课程笔记深入浅出地介绍了回归的基础概念、学习过程以及线性回归和逻辑回归的应用。对于初学者来说，这是一个很好的起点，可以帮助他们理解如何利用简单的数学模型解决实际预测问题。