平面直角坐标系详解：知识梳理与应用

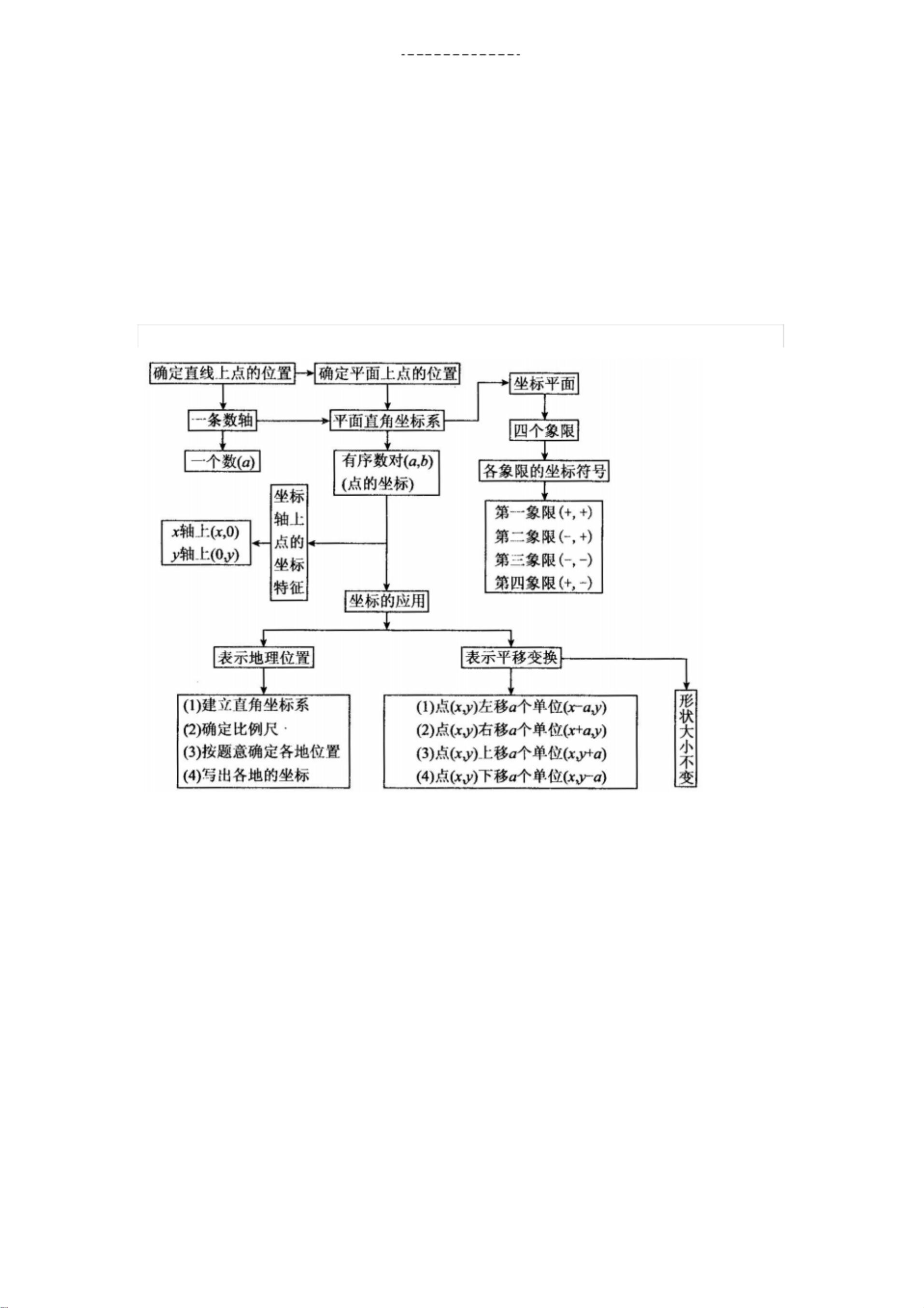
本资源主要涵盖了平面直角坐标系的相关知识，包括有序数对的概念、平面直角坐标系的构成和特点、坐标平面内的区域划分、点的坐标特性以及坐标系中的几何变换和距离计算等内容，旨在帮助学习者巩固这一章节的基础知识。 1. **有序数对**：有序数对是由两个数按照特定顺序组合而成，通常用于表示位置或特定的意义。例如，在电影院座位的示例中，(4, 5)表示第4排第5座。这种一对数的对应关系广泛应用于空间定位。 2. **平面直角坐标系**：由两条互相垂直的数轴组成，原点重合。坐标平面被分为四个象限（第一、第二、第三、第四）以及x轴和y轴。每个点在坐标系中对应一个唯一的有序数对（x, y），实现“形”与“数”的结合，方便进行代数与几何问题的转换。 3. **坐标平面的特性**： - 每个象限都有独特的坐标特征，例如，x轴上的点纵坐标为0，y轴上的点横坐标为0。 - 直线的平行性会影响点的坐标，平行于x轴的直线上的点纵坐标相同，平行于y轴的点横坐标相同。 - 点的对称性：关于x轴对称的点纵坐标互为相反数，关于y轴对称的点横坐标互为相反数，关于原点对称的点横、纵坐标都互为相反数。 - 象限角平分线上的点有特殊的坐标关系，一、三象限角平分线上点的横、纵坐标相等，二、四象限角平分线上点的横、纵坐标互为相反数。 4. **坐标表示距离**： - 点P(x, y)到x轴的距离是|y|，到y轴的距离是|x|。 - 在x轴上，两点A(x1, 0)和B(x2, 0)之间的距离AB等于|x1 - x2|；同样，y轴上的两点间的距离也类似计算。 这些内容是学习平面直角坐标系的基础，对于理解和应用坐标几何至关重要，能够帮助学生建立数形结合的思维，解决实际问题，如几何图形的位置关系、运动变化以及距离计算等。通过深入理解和熟练运用这些知识点，可以为进一步学习高级数学概念打下坚实的基础。