线性空间与矩阵论基础

"该资源是关于线性空间的讲解，主要针对矩阵论的学习者，介绍了线性空间的基本概念、性质以及与数域的关系。" 线性空间是线性代数的核心概念，它在数学和工程领域有着广泛的应用，特别是在矩阵论中。线性空间是一种结构化的集合，集合中的元素称为向量，而数域则是定义在这些向量上的运算背景。在矩阵论中，理解和掌握线性空间的性质是至关重要的。 首先，线性空间的定义包括两个主要组成部分：一个非空集合V和一个数域F。集合V的元素可以是任何类型的事物，如向量、函数、矩阵等，而数域F则是一个对四则运算封闭的数集，如有理数、实数或复数。线性空间的特性主要体现在定义在V上的两个运算——加法和数乘： 1. 加法运算具有以下性质： - 结合律：对于任意向量u, v, w，都有(u + v) + w = u + (v + w)。 - 交换律：向量的加法是可交换的，即u + v = v + u。 - 存在零元素o：加零向量于任何向量后结果不变，即u + o = u。 - 存在负元素：每个向量u都有一个相反数-u，使得u + (-u) = o。 2. 数乘运算也有特定规则： - 数因子分配律：对于任意标量α和向量u, v，都有α(u + v) = αu + αv。 - 分配律：对于任意标量α, β和向量u，有(α + β)u = αu + βu。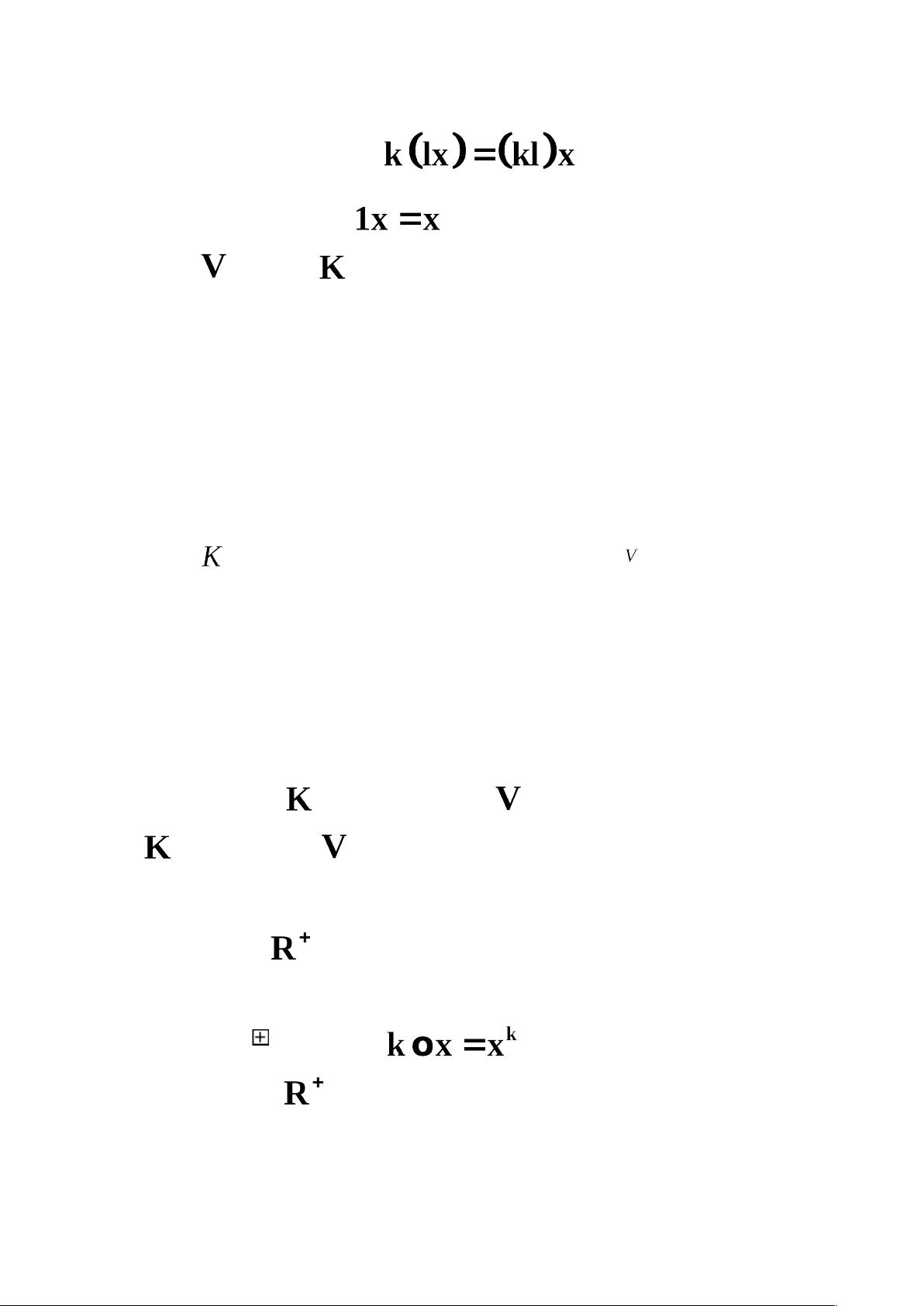 - 结合律：标量乘法满足α(βu) = (αβ)u。 - 恒等律：标量1乘以任何向量u等于u本身，即1u = u。 线性空间的这两个运算必须满足以上8条性质，并且它们必须在集合V上是封闭的，即任意两个向量的加法结果和标量与向量的乘积结果仍属于V。此外，这里的加法和数乘与通常的集合运算有所不同，它们更为抽象，不局限于传统的集合运算概念。 当数域F是实数域R时，我们称这样的线性空间为实线性空间；若F是复数域C，则称其为复线性空间。例如，所有二维实数向量构成的集合就是一个典型的实线性空间。 在给定的文件内容中，还提到了一个具体例子：集合V由全体正实数组成，定义了新的加法和数乘运算。这个集合虽然看似简单，但它的加法和数乘运算并不符合线性空间的封闭性，因为两个正实数相乘可能得到非正实数，这违反了数乘的封闭性，因此这个集合不能构成一个线性空间。 总结来说，线性空间是数学中一个基本的概念，它提供了一个框架来研究向量的加法和标量乘法，是矩阵论和其他许多数学分支的基础。理解线性空间的定义、性质以及与数域的关系，对于深入学习线性代数和矩阵论至关重要。