变分自编码器VAE原理详解与应用

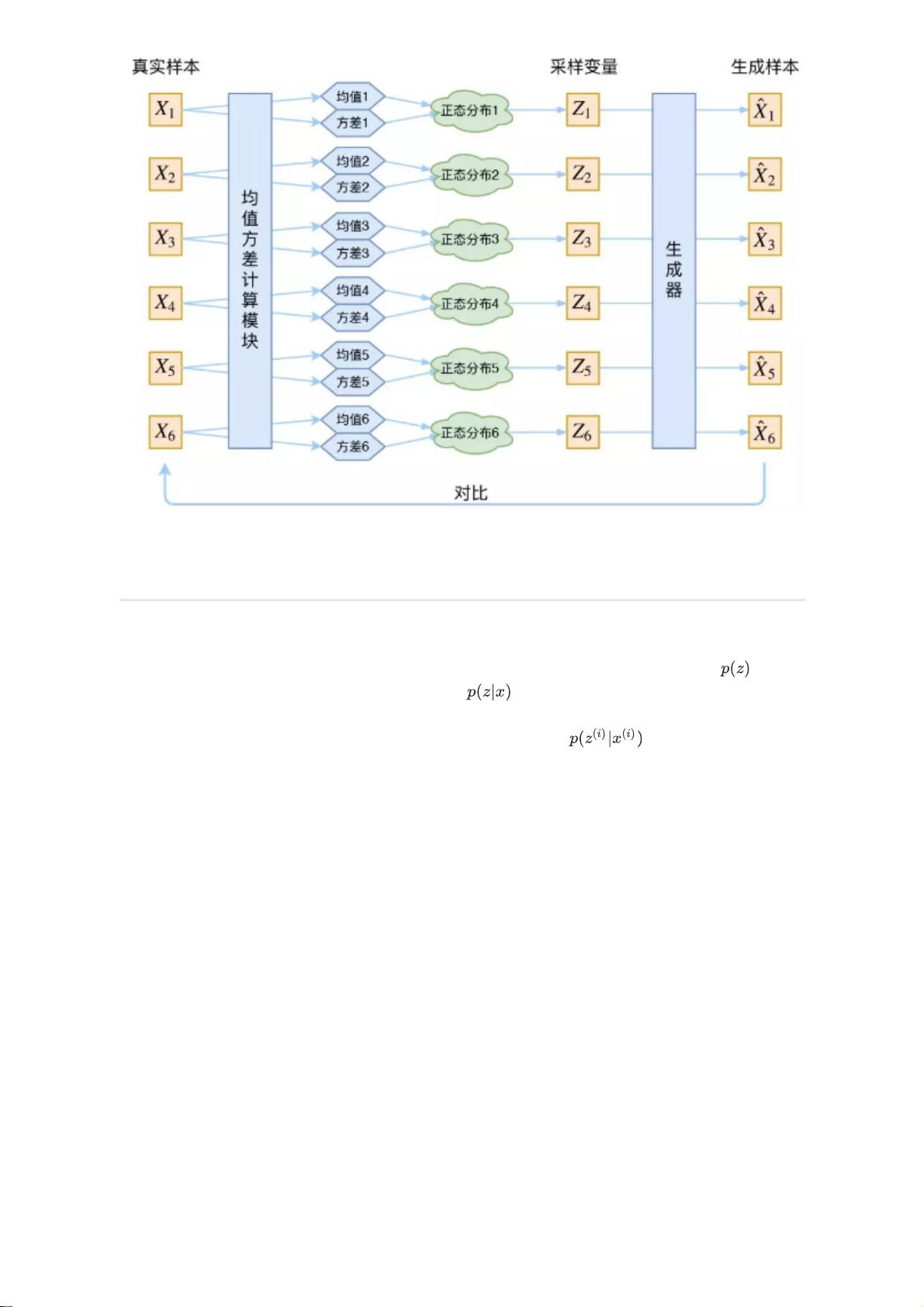
"这篇文章主要解析了变分自编码器（VAE）的原理，包括其基本形式、数学基础以及理解中的关键点。VAE是一种生成模型，旨在通过学习数据的潜在分布来生成新的样本。文章指出，VAE的核心是通过建立隐变量与观测数据之间的关系，来近似真实数据分布，并利用变分推理方法解决生成分布与真实分布之间的相似度衡量问题。" 1. **VAE的形式** VAE是一种生成模型，它的目标是学习数据的潜在分布，从而能够生成与训练数据类似的新样本。在这个框架下，数据样本`x`与其关联的隐变量`z`共同描述了一个生成过程，其中`p(z)`是隐变量的先验分布，通常假设为标准正态分布，而`p(x|z)`是给定隐变量时生成数据的概率。 2. **数学原理** 在VAE中，由于直接获取数据的真实分布`p(x)`很困难，模型通过引入后验分布`p(z|x)`来间接逼近。后验分布描述了给定观测数据`x`时，隐变量`z`的分布。VAE的目标是通过最大化后验概率`p(x) = ∫ p(x|z)p(z) dz`来学习模型参数。然而，这个积分通常是不可解的，因此VAE采用变分推理，引入一个易于处理的近似后验分布`q(z|x)`，并试图最小化KL散度`D_{KL}(q(z|x)||p(z|x))`，同时最大化证据下界（ELBO）。 3. **生成过程与衡量指标** VAE的生成过程包括两步：首先，从标准正态分布`p(z)`中采样得到隐变量`z`；然后，使用神经网络预测生成数据的概率`p(x|z)`。为了评估生成分布`p(x)`与真实分布`p_data(x)`的相似度，VAE使用ELBO作为优化目标，它是负向KL散度和期望重构误差的组合。重构误差通常采用L2距离，但直接从先验分布采样`z`可能导致无法对应到真实样本`x`的问题。 4. **变分推理** 解决上述问题的方法是，在训练时，VAE不直接从先验`p(z)`采样，而是从数据驱动的近似后验`q(z|x)`采样。通过一个称为“解码器”的神经网络，可以预测给定`x`时的`z`分布，然后从中采样得到`z`。这样，每个真实样本`x`都与一个特定的`z`值相关联，使得生成的样本更可能对应于真实样本。 5. **VAE的实现与应用** VAE在实际应用中，如图像生成、文本生成等领域有广泛的应用。由于其内在的随机性，VAE可以生成多样性的输出，同时，通过学习数据的潜在空间，还支持对数据进行有意义的编辑和操作。 6. **参考资料** 文章列举了多篇参考文献，包括不同角度解析VAE的文章，如从贝叶斯观点出发的解释，以及李宏毅教授的机器学习讲义，这些资源可以帮助深入理解VAE的原理和实现细节。 通过这些讲解，我们可以了解到VAE作为一种有效的生成模型，其理论基础、训练策略以及在机器学习中的应用价值。理解VAE的关键在于把握其变分推断的机制，以及如何通过优化ELBO来学习数据的潜在表示。