AVL树详解：平衡二叉树的关键与操作优化

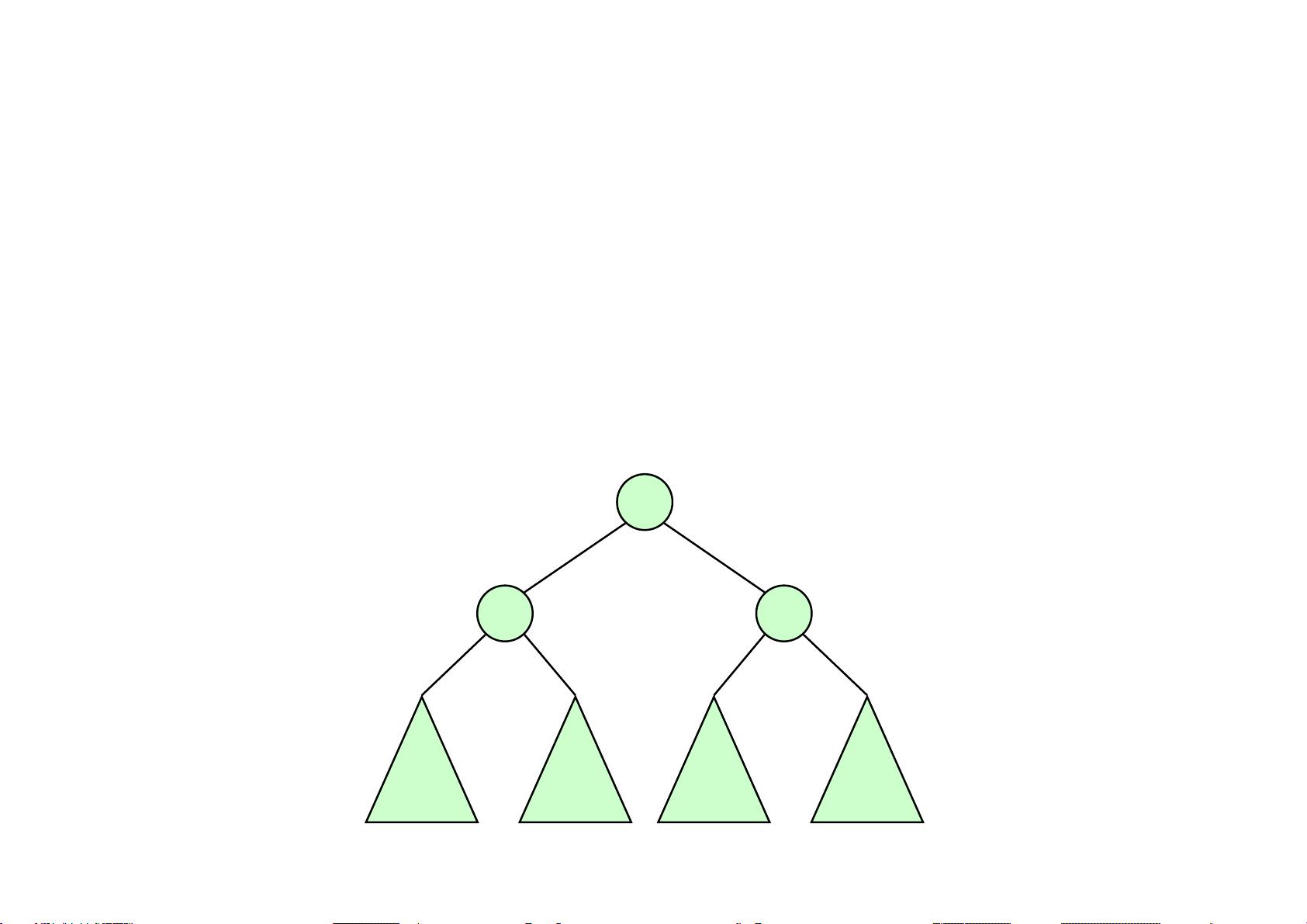
平衡二叉树，又称AVL树，是一种自平衡的二叉搜索树，它的核心在于维护树的平衡性，确保对树中任意节点的查找、插入和删除操作的时间复杂度保持在最优化状态。以下是关于AVL树的详细介绍： 1. **基本概念**: - **基本BST**：二叉搜索树(BST)的基本定义包括左子树小于根节点，右子树大于根节点，且左右子树都是BST。操作上，查找、插入和删除的时间复杂度分别与树的高度成正比，非平衡情况下可能导致效率降低。 2. **平衡的重要性**： - 平衡二叉树的关键在于树的高度尽可能小，这样可以保证搜索、插入和删除等操作的平均时间复杂度接近于对数时间（O(log n)），这对于大规模数据集尤其关键。当树高度过高时，操作性能会急剧下降。 3. **AVL树的定义**： - AVL树的定义是每个节点的左右子树高度差不超过1，这通过在插入和删除后通过旋转操作来维护。空树的高度定义为-1，这是平衡的边界条件。 4. **AVL树的高度计算**： - AVL树的高度可以通过数学公式表示，如S(n)表示高度为n的最少节点数，满足递推关系S(n) = S(n-1) + S(n-2) + 1。通过斐波那契数列的性质，可以证明AVL树的最大高度大约为log2(n)。 5. **旋转操作**： - 当树不平衡时，通过单旋转和双旋转操作来调整。单旋转分为左旋和右旋，分别对应祖父节点与孙子节点共线或不共线的情况。旋转操作的目的是将高度差恢复到1以内，保证平衡。 6. **插入算法**： - 插入元素时，从目标位置开始向上遍历，找到第一个祖父节点不满足平衡条件的点x，然后进行相应的旋转操作，以最小化高度差。这个过程确保了插入操作的高效性。 AVL树是一种高度优化的二叉搜索树，通过严格的平衡规则和旋转机制，保证了查找、插入和删除操作的最优时间复杂度，是计算机科学中的一个重要数据结构。理解并掌握AVL树的原理和操作对于处理大量数据的场景至关重要。