轴测投影公式详解:定理、应用与计算
需积分: 10 76 浏览量
更新于2024-08-12
收藏 178KB PDF 举报
轴测投影是画法几何学中的核心概念,它涉及将三维空间的物体映射到二维平面上,以直观地展示其形状和尺寸关系。本文主要讨论的是"轴测投影的基本公式及其应用",发表于2001年5月的东南大学学报(自然科学版)。作者唐人卫教授通过解析方法,深入研究了轴测投影系统中的关键要素,包括空间坐标系、投射方向和投影面之间的几何关系。
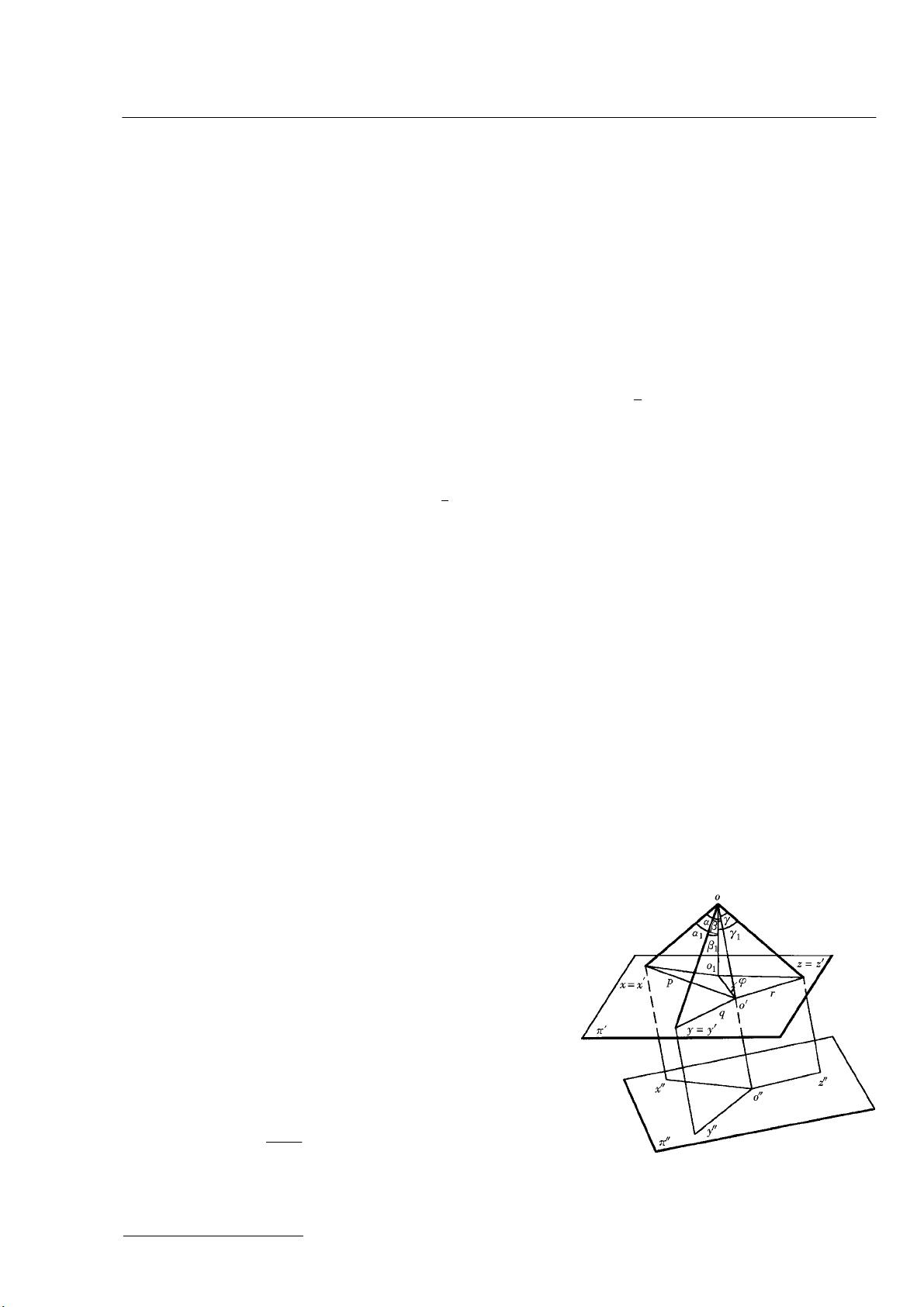
轴测投影的基本定理,也称为波尔克许华尔兹定理,是本文的核心理论基础。它阐述了如何在平面投影中,通过轴测轴的设置和轴向伸缩系数的选择,实现空间坐标轴与轴测投影之间的对应关系。该定理指出,轴测轴间的角度和轴向伸缩比例直接决定了投影的精确度和比例,且这些参数之间存在着明确的定量关系。
文章的核心成果是推导并证明了轴测投影的基本公式,即公式(1):
(pqsin∠x′o′y′)² + (qrsin∠y′o′z′)² + (rpsin∠z′o′x′)² = p² + q² + r² - 1
在这个公式中,p、q、r分别代表轴向伸缩系数,而∠x′o′y′、∠y′o′z′、∠z′o′x′则是轴测轴间的角。这个公式定量地表达了轴测参数之间的关系,使得在实际应用中,可以根据给定的轴测参数计算出相应的空间坐标轴位置和投射方向。
通过这个公式,作者整理出了适用于正轴测投影和斜轴测投影的五组参数计算公式,这对于工程制图、建筑设计、机械设计等领域具有重要意义,能够帮助设计师和工程师准确地进行三维模型到二维图纸的转换,提高设计效率和精度。
总结来说,这篇文章不仅深化了对轴测投影原理的理解,还提供了实用的计算工具,对于推动画法几何学的教学和实践应用具有重要的价值。
2021-09-25 上传
2021-08-19 上传
2021-08-06 上传
171 浏览量
125 浏览量
点击了解资源详情
点击了解资源详情
2025-03-06 上传
weixin_38592643
- 粉丝: 2
最新资源
- 掌握PerfView:高效配置.NET程序性能数据
- SQL2000与Delphi结合的超市管理系统设计
- 冲压模具设计的高效拉伸计算器软件介绍
- jQuery文字图片滚动插件:单行多行及按钮控制
- 最新C++参考手册:包含C++11标准新增内容
- 实现Android嵌套倒计时及活动启动教程
- TMS320F2837xD DSP技术手册详解
- 嵌入式系统实验入门:掌握VxWorks及通信程序设计
- Magento支付宝接口使用教程
- GOIT MARKUP HW-06 项目文件综述
- 全面掌握JBossESB组件与配置教程
- 古风水墨风艾灸养生响应式网站模板
- 讯飞SDK中的音频增益调整方法与实践
- 银联加密解密工具集 - Des算法与Bitmap查看器
- 全面解读OA系统源码中的权限管理与人员管理技术
- PHP HTTP扩展1.7.0版本发布,支持PHP5.3环境