神经网络基础：模型、函数与学习算法

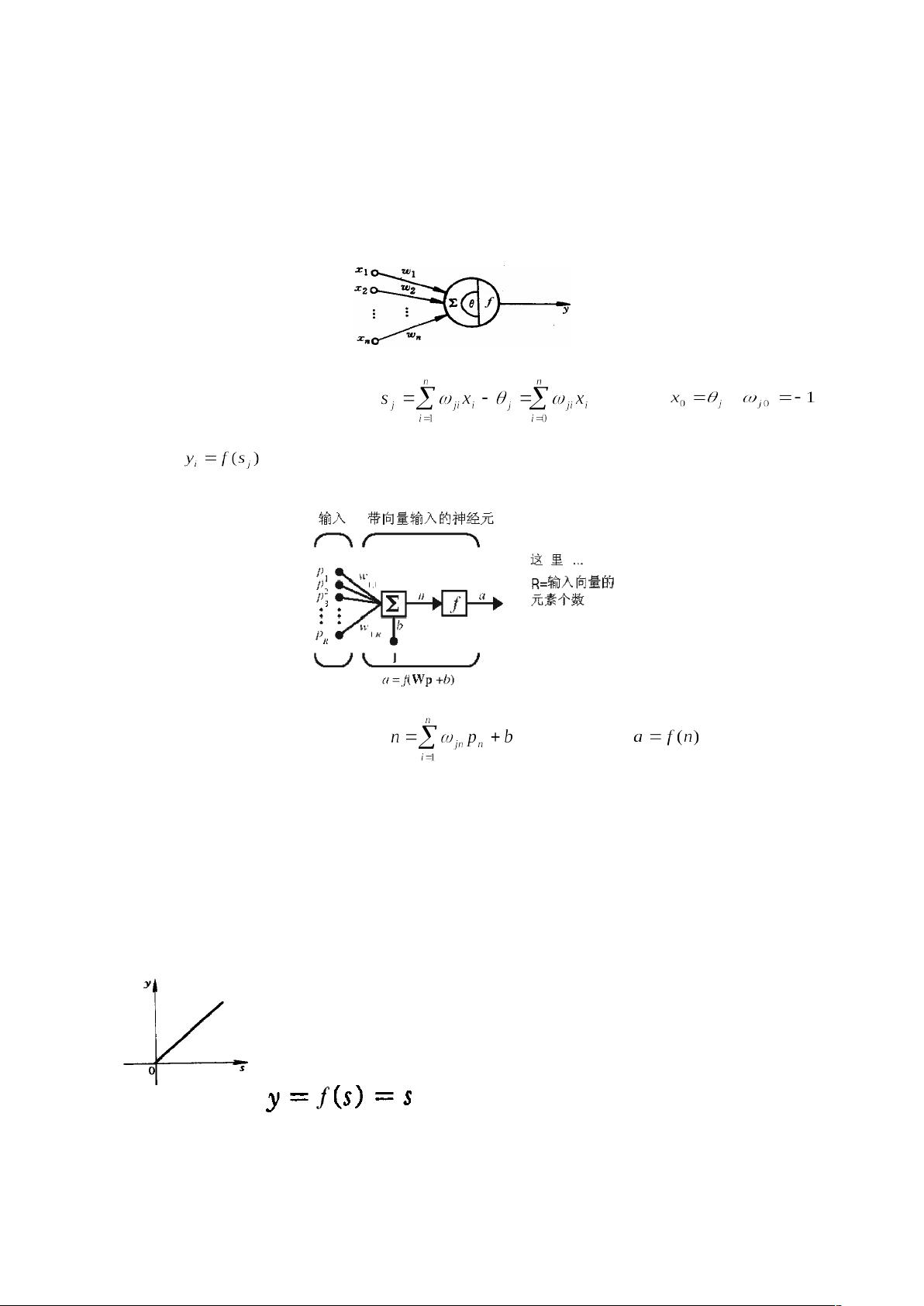
"神经网络概述，包括生物神经元、人工神经网络结构、常见的神经元变换函数、神经网络的发展、目的意义、应用、局限性以及基本学习算法。" 神经网络是模拟生物神经系统的计算模型，用于解决复杂的学习和识别任务。在生物神经元部分，我们了解到神经元是如何接收输入信号并产生输出的。人工神经网络（ANN）则是基于这种生物学概念建立的数学模型，其基本结构由输入层、隐藏层和输出层组成。输入层接收数据，隐藏层处理信息，而输出层则产生结果。 通用模型通常表示为一个加权求和的过程，每个输入xi与相应的权重w乘后相加，加上阈值θ，通过响应函数转化为输出yi。这个响应函数，也称为激活函数，决定了神经元是否被“激活”以及激活的程度。在MATLAB仿真中，我们可以看到类似的模型，其中权值和阈值可以通过训练来调整，以优化网络性能。 响应函数的选择对神经网络的性能至关重要。常见的函数包括线性单元（比例函数）、符号函数、饱和函数、双曲函数、阈值单元（阶跃函数）以及S型（Sigmoid）函数。这些函数具有不同的特性，例如线性单元提供连续变化的输出，符号函数用于二分类问题，而Sigmoid函数则常用于输出概率。 神经网络的研究发展主要集中在误差反传算法（BP网络），它在函数逼近、模式识别、分类和数据压缩等领域广泛应用。尽管BP网络有效，但也有其局限性，如梯度消失和局部极小点问题。 神经网络的学习算法多种多样，包括指导式学习（监督学习）、非指导式学习（无监督学习）和强化学习。其中，Hebb学习规则是无监督学习的一种，它的核心思想是连接权重的更新与神经元的活动相关联。其他学习规则如感知器学习规则、最小均方学习规则等，都是为了优化网络性能和收敛速度。 神经网络是一个强大且灵活的工具，能够适应各种复杂问题，但同时也需要深入理解其内部工作机制，如激活函数的选择和学习算法的运用，才能有效地设计和训练神经网络模型。随着技术的不断发展，神经网络的应用将持续扩展，为人工智能领域带来更多的创新和突破。