使用分支限界法解决旅行加油优化问题

"《算法分析与设计》课程的分支限界法作业，涉及旅行加油问题和贪吃蛇走迷宫问题。作业要求包括编写目标函数、限界函数、约束函数，绘制解空间树、搜索空间树及堆变化，分析时间复杂度，并用C/C++编程实现。题目1是帮助小李规划最省钱的自驾游路线，考虑不同城市的汽油价格，汽车单位距离耗油1单位，需给出输入城市数量、道路数量、汽油价格、城市间距离、油箱容量、出发和终点信息，输出最低费用。" 在这个作业中，主要的知识点包括： 1. **分支限界法**：这是一种全局最优搜索策略，通过扩展解空间树的分支来寻找问题的最优解。它通常用于解决组合优化问题，如旅行商问题、0-1背包问题等。在本题中，我们需要设计分支限界法来解决旅行加油问题。 2. **目标函数**：在旅行加油问题中，目标函数代表我们想要最小化的费用。对于每个节点，我们需要计算当前路径的总成本，包括已经消耗的汽油费用和剩余油量不足以到达下一个城市的额外加油费用。 3. **限界函数**：限界函数用于剪枝，减少不必要的搜索。在每次扩展节点时，如果该节点的潜在解（如加上预期的油费）比当前已知的最优解还要差，那么可以直接剪掉这个分支，避免进一步探索。 4. **约束函数**：约束函数确保搜索过程始终在合法的解空间内。例如，汽车的油量不能为负，必须足够支撑到达下一个城市，且不能超过油箱的最大容量。 5. **解空间树与搜索空间树**：解空间树是由所有可能的解构成的树形结构，而搜索空间树是在解空间树基础上，根据搜索策略（如广度优先或深度优先）进行扩展的部分。在旅行加油问题中，每个节点可能代表一个城市，连接表示路径，节点的值包括当前油量、总成本等信息。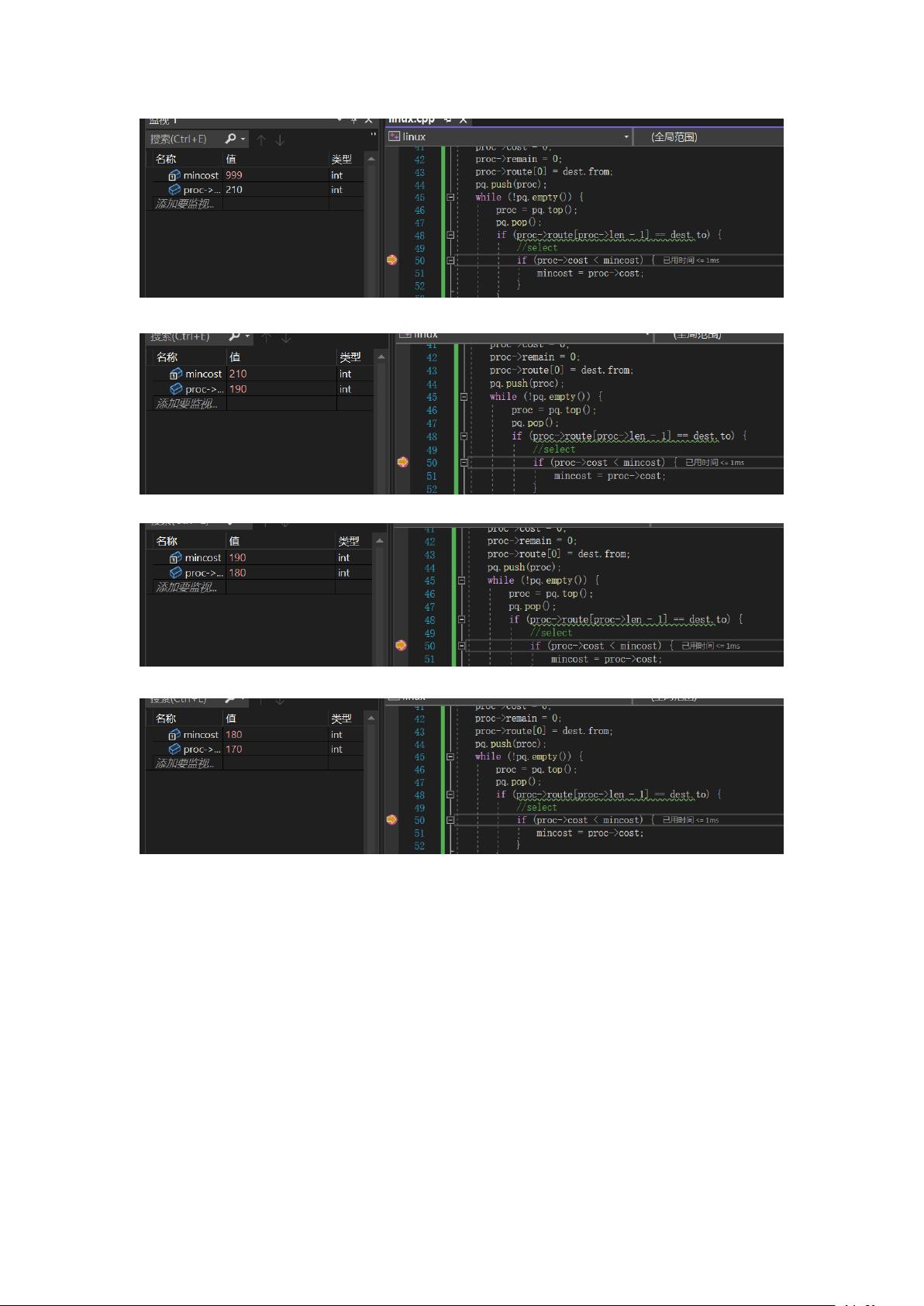 6. **堆的变化**：在分支限界法中，通常使用优先队列（如最小堆）来存储待处理的节点。随着搜索的进行，堆中的节点会根据目标函数的值进行调整，保证每次处理的节点都是当前最优的。 7. **时间复杂度分析**：虽然分支限界法的复杂度通常与问题的规模相关，但具体到本题，可能需要考虑城市的数量、道路的数量以及油箱的容量等因素对算法运行时间的影响。 8. **C/C++编程实现**：编程实现需要将上述理论转化为具体的代码逻辑，包括读取输入、计算目标函数、应用限界函数、构建和维护搜索空间树，以及输出结果。 9. **贪吃蛇走迷宫问题**：尽管题目主要聚焦于旅行加油问题，但提到了贪吃蛇走迷宫问题，这可能是另一个分支限界法的应用实例，需要找到从起点到终点的最短路径，考虑到蛇的移动规则和迷宫的结构。 这份作业涵盖了分支限界法的基本概念和应用，要求学生不仅理解算法原理，还要具备实际编程解决问题的能力。