SPSS非参数检验全解析：从Chi-Square到K RelatedSamples

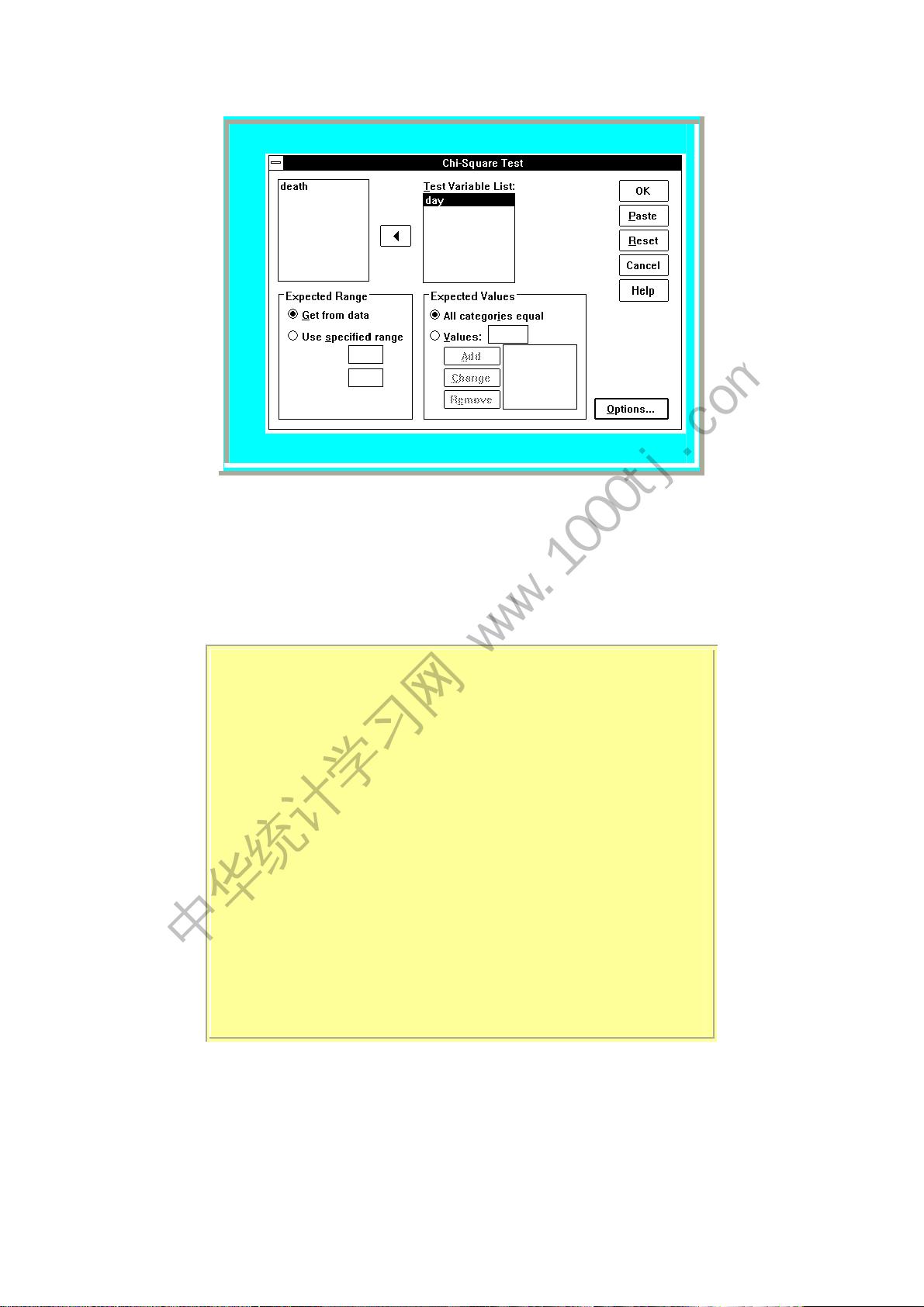
"本资源是关于统计软件SPSS在非参数检验中的应用教程，主要讲解了 Chi-Square、Binomial、Runs、1-Sample K-S、2 Independent Samples、k Independent Samples、2 Related Samples 和 K Related Samples 等一系列非参数检验过程。教程来自圣才学习网，适合对SPSS和非参数检验感兴趣的学者或研究人员学习。" 非参数检验是一种不依赖于总体特定分布假设的统计分析方法，它广泛应用于那些总体分布未知或难以满足正态分布等特定分布条件的数据中。SPSS作为一款强大的统计分析软件，提供了多种非参数检验工具，使得用户能够对各种类型的数据进行有效的分析。 首先，Chi-Square过程用于进行配合度检验，评估实际观察频数与期望频数之间的差异，例如在检验各组间的比例是否相等或者分类变量之间是否存在关联时。实例中，通过比较一周内各天的死亡数来判断死亡危险性是否相同。 接下来，Binomial过程适用于二项分布检验，当研究的是两个可能结果（成功或失败）的独立试验次数时，可以使用此过程。 Runs过程则是用来检验序列中的趋势，比如判断随机序列是否存在某种模式。 1-Sample K-S（Kolmogorov-Smirnov检验）和2 Independent Samples过程分别用于单样本和两独立样本的分布检验，检查样本是否来自于同一分布。1-Sample K-S检验一个样本数据与理想分布的差距，而2 Independent Samples则对比两个独立样本的分布差异。 k Independent Samples过程则扩展到多个独立样本的情况，用于比较三个或更多独立样本的分布。 2 Related Samples和K Related Samples过程则是针对配对或相关样本的非参数检验，比如检验两组相关样本的分布差异，通常用于配对设计的研究。 在进行非参数检验时，虽然它们不需要严格的分布假设，但要注意的是，这种方法的检验效能通常低于参数检验，即在相同条件下，可能需要更大的样本量才能获得同样的统计功效。因此，在选择非参数检验时，需要综合考虑数据的特性、研究目的以及可能损失的信息量。 通过SPSS提供的这些非参数检验工具，用户可以轻松进行各种非参数分析，无论是单样本还是多样本，无论是独立样本还是配对样本，都能找到相应的检验方法，从而对数据进行深入的探索和推断，得出科学的结论。在实际操作中，理解每个过程的主要功能，并结合实例操作，能帮助用户更熟练地运用SPSS进行非参数检验。