二维椭圆边值问题的线性有限元导数恢复与超收敛性分析

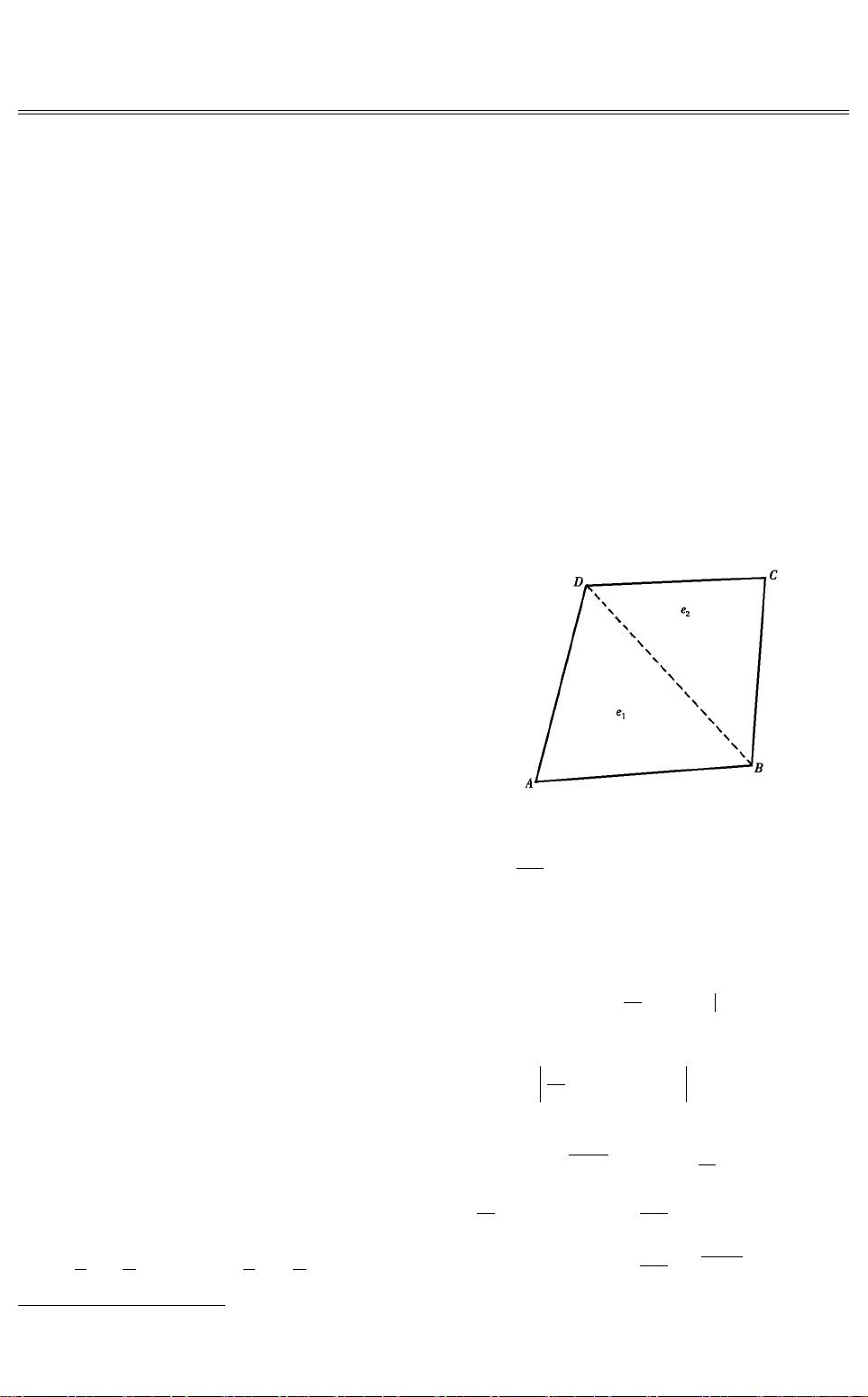
"该文研究了线性有限元在解决二维椭圆边值问题时的导数恢复技术，特别关注于线性三角元、双线性矩形元和四边形元。文中提出三种有限元导数恢复公式，用于计算剖分节点处的导数，并具有超收敛性质。这些恢复公式在不增加过多计算负担的情况下，能够提供高精度的节点导数计算值。" 线性有限元方法是数值分析中解决偏微分方程的一种常用工具，尤其在工程和科学计算中广泛应用。然而，线性有限元的导数在节点处通常不连续，这给直接获取节点导数值带来了挑战。为解决这一问题，论文提出了导数恢复技术，包括Z-Z导数小片恢复技术和导数插值恢复技术。 文章重点在于构建了针对二维椭圆边值问题的线性三角元、双线性矩形元和四边形元的三种导数恢复公式。这些后处理公式允许我们通过有限元解间接计算出剖分节点处的导数值，并且表现出超收敛性，即它们的误差比传统的有限元解的误差下降得更快。 对于线性三角元，论文首先考虑了有限元空间的定义，然后构建了相应的导数恢复公式。这类公式的建立基于近似平行四边形的概念，通过对相邻边长的控制来确保恢复精度。 双线性矩形元和四边形元的处理则涉及到更复杂的几何结构。论文中指出，尽管四边形单元在实际问题中更常见，但其导数恢复的处理相对复杂，需要考虑边界的对称性和单元形状的扭曲程度。 所有这些恢复公式都具有简单明了的特点，且计算量增加不大，这使得它们在实际应用中更具吸引力。通过这些技术，可以提高有限元解的精度，特别是在需要精确导数信息的场合，如在优化设计、流体动力学或者材料科学等领域。 这篇2002年的论文对线性有限元导数恢复技术的理论和实践进行了深入探讨，提供了实用且高效的算法，对于理解和改进有限元方法在求解偏微分方程中的性能具有重要意义。其贡献在于不仅提供了新的计算方法，还展示了这些方法的超收敛性，这对于数值计算的精度提升有着显著的促进作用。