二分三分哈希详解：搜索、排序与散列技术

二分三分哈希是一种在数据结构和算法中常用的搜索技术，它结合了二分查找和散列的概念。首先，我们来看看二分查找。 **二分查找**（Binary Search）是一种在有序数组中查找特定元素的高效算法。它的工作原理基于分割和比较：从中间元素开始，如果目标值小于中间元素，则在左半部分继续查找；如果目标值大于中间元素，则在右半部分查找，以此递归进行，直至找到目标值或者搜索范围为空。这种方法的时间复杂度是O(log n)，因为它每次都将搜索范围减半，对于包含n个元素的数组，查找次数最多为log2(n)次。在C++标准模板库(STL)中，`std::binary_search`函数实现了这一功能，可用于检测一个元素是否存在于已排序的范围中。 接下来是**三分查找**（Three-Way Partitioning），虽然这个词组可能更常用于解决排序问题（如快速排序的分区操作），但它在此处指的可能是寻找凸性函数的极值，类似于二分查找但扩展到了寻找峰值或者谷值。在某些数学优化问题中，这种查找方法可以帮助定位函数的最大值或最小值，尤其是在连续函数且变化趋势已知的情况下。 然后是**哈希**（Hash），这是一种数据结构和算法的重要组成部分，它的核心思想是将任意长度的输入通过散列函数转换成固定长度的输出，即散列值。散列函数的设计目标是保证输入的任何变化都会导致输出值有显著的变化，从而实现快速查找和存储。哈希表（Hash Table）就是基于哈希函数设计的数据结构，常用于实现高效的查找、插入和删除操作，平均时间复杂度接近O(1)。然而，由于哈希冲突的存在，处理不当可能导致性能下降，因此需要通过合适的哈希函数和冲突解决策略（如开放寻址法或链地址法）来优化。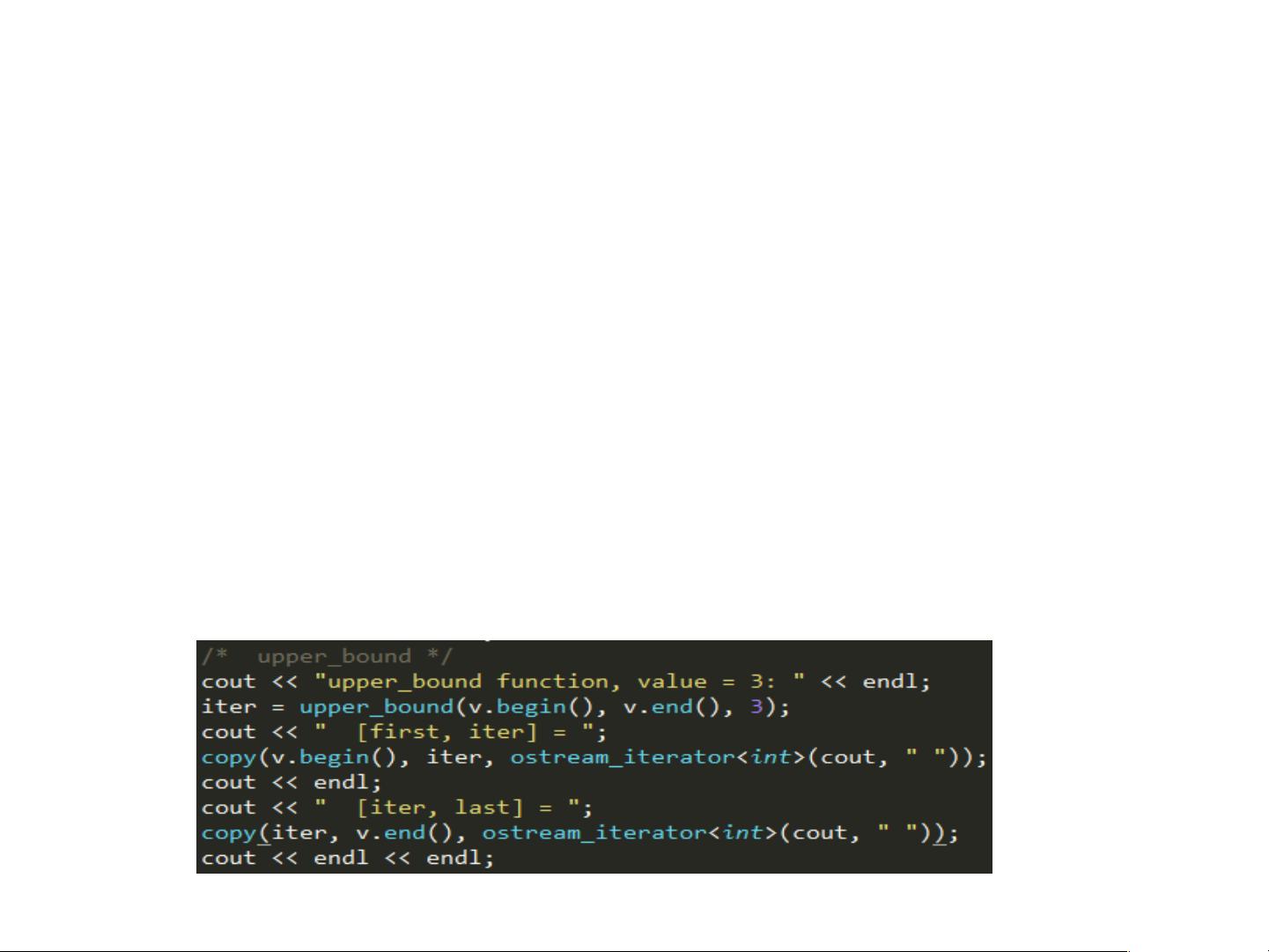 STL中的`std::lower_bound`、`std::upper_bound`和`std::equal_range`是一组用于有序容器的操作，它们分别用于查找第一个大于或等于目标值的位置、第一个大于目标值的位置以及目标值在序列中的起止范围。这些函数在哈希查找和区间定位中有广泛应用，例如在离散化、区间搜索和数据预处理时能提高效率。 总结来说，二分三分哈希包含了二分查找的高效搜索策略，以及哈希函数在数据结构中的应用，特别是在处理有序数据和寻找特定位置时。理解这些概念和算法的细节，有助于我们在实际编程中设计出更加高效的数据处理方案。