离散点插值与等值线绘制技术在VB6.0中的实现

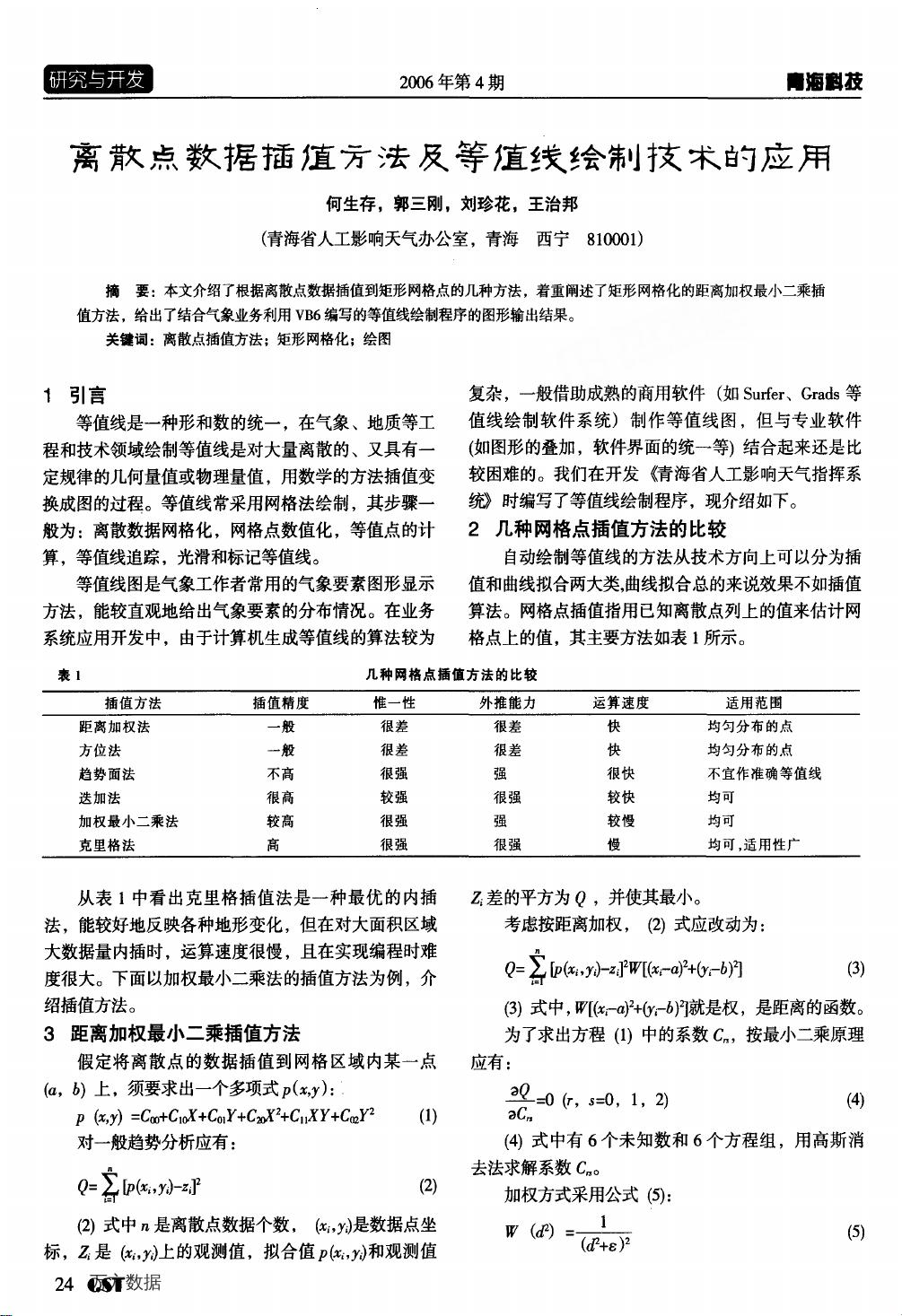
"本文主要介绍了离散点数据插值方法以及如何使用矩形网格法来绘制等值线，尤其在VB6.0环境下实现的算法。文中提到了距离加权最小二乘插值方法，并通过实例展示了两种软件绘制等值线的比较。此外，还简述了如何利用网格法绘制立体表面图，包括坐标系的转换过程。" 离散点数据插值是一种在计算机图形学和数据分析中常见的技术，用于填补数据点之间的空缺，构建连续的表面或曲线。在本文章中，作者讨论了一种特定的插值方法——距离加权最小二乘插值，这种方法考虑了离散数据点到目标网格点的距离，以确定最佳的插值结果。插值的目标是使得插值后的函数在所有离散点上的误差平方和最小。 等值线绘制是插值应用的一个重要方面，它用于表示具有相同特征值的区域，例如地理上的等高线或气象学中的等温线。在矩形网格法中，首先将数据所在的区域划分为网格，然后在每个网格内使用插值算法估算数据值。等值线的追踪和搜索则涉及到判断等值线在网格中的走向和出边，以便连成完整的线条。文章指出，等值线可能有四种基本走向，并且在追踪过程中需要避免复杂的判断情况。 VB6.0被用来实现这一算法，这是一种早期的Microsoft Visual Basic版本，用于开发Windows应用程序。通过VB6.0，作者实现了等值线的追踪和填充功能，可以生成开曲线和闭合曲线的等值线图。文章通过两个实例（分别使用SUrfer和VB6编程）展示了等值线图的绘制效果，尽管两者在等值线的密集程度上有所不同，但走向一致。 此外，文章还简要讨论了如何将这些方法扩展到三维空间，即利用网格法绘制立体表面图。这涉及到坐标系的转换，将原始的直角坐标系转换为新的坐标系，以便进行投影。转换公式包含了旧坐标系和新坐标系之间轴的方向余弦，确保了坐标变换的准确性。 这篇文章除了介绍离散点插值的基本概念和等值线绘制的技术细节外，还提供了实际应用的例子，展示了如何在实际编程环境中实现这些理论概念。这对于理解和应用这些技术到实际的数据分析和可视化项目中具有指导意义。