高斯伪谱法:理论、优化与应用
"高斯伪谱法是一种数值计算方法,主要用于解决优化问题,特别是与动力学模型相关的最优控制问题。这种方法结合了积分和微分形式,通过离散化过程转化为非线性规划问题(NLP)。高斯伪谱法由David Benson在2004年提出,并由Geoffrey Todd Huntington在2007年进一步发展和完善。该方法的一个关键优势是能够提供高精度的协态变量估计,这对于验证解的最优性、进行敏感性分析以及网格细化至关重要。
高斯伪谱法的理论基础包括以下几个方面:
1. **等价性证明**:Benson证明了无论积分形式还是微分形式的最优控制问题,离散后的NLP问题与两点边值问题(HBVP)的离散形式等价。这意味着通过解决NLP问题,可以直接满足传统的间接法最优性条件。
2. **协态变量的处理**:高斯伪谱法通过KKT条件与HBVP的离散形式的等价性,能够直接计算协态变量的估计值,尤其是在边界点上具有极高的精度。这对于优化问题的解的验证和状态对价值函数的敏感性分析非常有用。
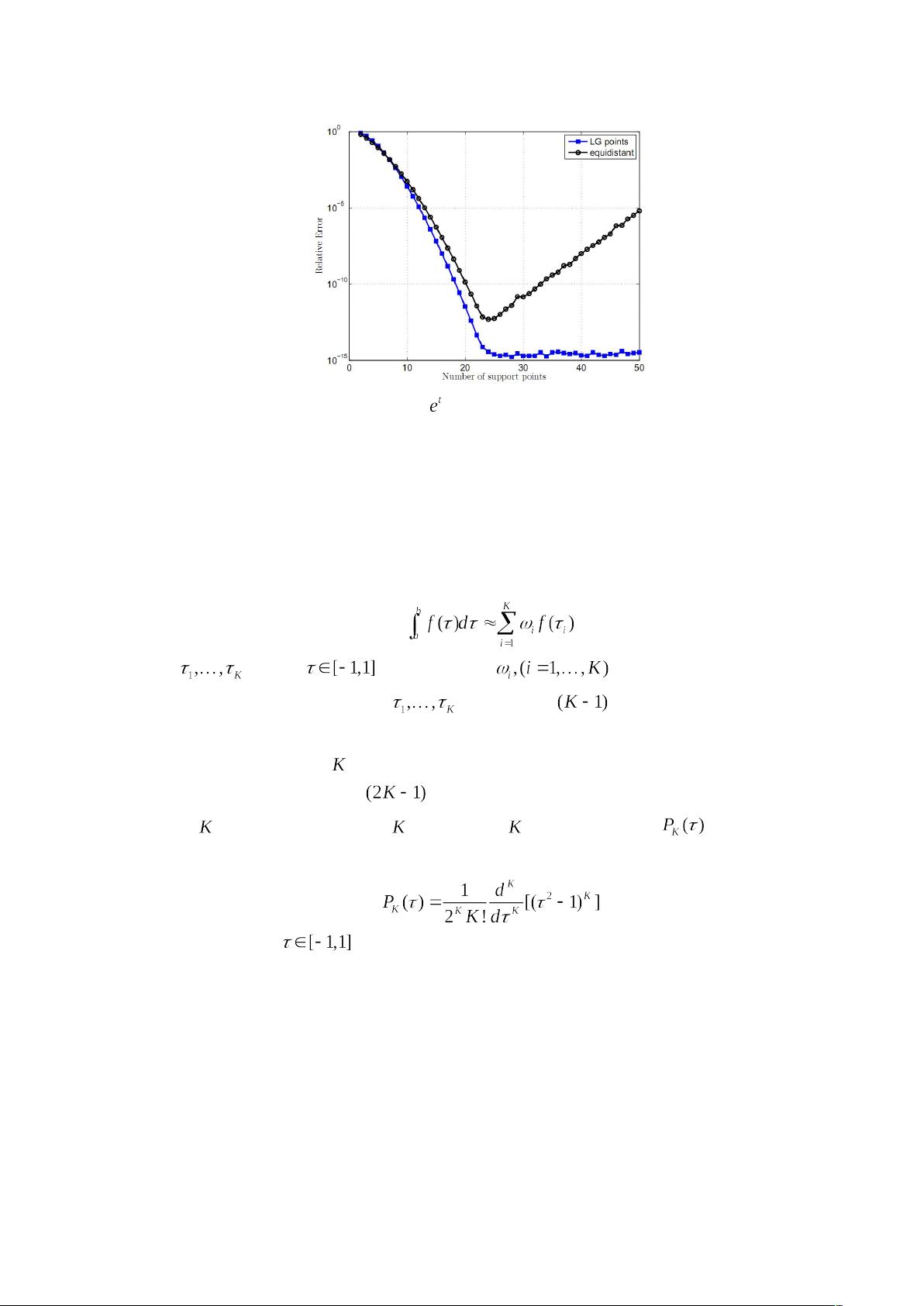
3. **稀疏矩阵的优势**:高斯伪谱法使用插值代替积分,构建出稀疏的约束雅克比矩阵,这有利于数值优化算法的高效求解。它能够在较少的离散点上,以较快的速度和较高的精度找到优化问题的解。
4. **实时优化潜力**:由于其快速的求解速度和精确的协态变量估计,高斯伪谱法被认为是实时优化控制器设计的有力工具。它可以用于构造一定精度的实时控制系统,这在很多工程应用中具有重要意义。
在实际应用中,高斯伪谱法通常涉及以下步骤:
- **模型离散化**:将连续的动力学模型转化为离散的非线性规划问题。
- **插值构造**:利用高斯节点和基函数构建插值函数,形成稀疏的系统矩阵。
- **优化求解**:通过数值优化算法解决NLP问题,得到控制量和状态变量的最优解。
- **协态变量估计**:利用KKT条件计算协态变量,进行解的验证和敏感性分析。
- **结果后处理**:根据边界条件和解的特性,可能需要对结果进行细化或重构。
高斯伪谱法提供了一种有效且精确的手段来解决复杂的动态优化问题,特别是在航空航天、机械工程、自动化控制等领域有广泛的应用前景。它的高效性和准确性使其成为数值计算和控制理论中一个重要的工具。"
832 浏览量
476 浏览量
257 浏览量
613 浏览量
sd4574462
- 粉丝: 2
- 资源: 1
最新资源
- TWinSoftSetup_11.00.1347编程软件.zip
- statisticalModel:这是为了存储统计模型
- VR-Viz:基于A框架的React组件,用于VR中的数据可视化
- 基于HTML实现的宽屏大气咖啡商店响应式网站模板5293(css+html+js+图样)
- 技嘉B460M小雕Elite+10400.zip
- bulid_new.rar
- passwordGenerator
- USB_PPM_Joystick:Arduino适配器,用于RC远程控制PPM信号到USB HID游戏杆
- 正泰NIOG1Y系列油田抽油机节能变频柜.rar
- code码
- Xshell连接工具 XshellXftpPortable.zip
- The-Brooding-Fighting-Forces
- Archity-开源
- 罗克韦尔自动化半导体与电子行业FMCS系统解决方案.zip
- 家纺用品网上销售管理系统-毕业设计
- uri-judge:C ++中的URI判断问题(cpp)