LINGO18.0教程:交互式优化求解器详解
需积分: 15 57 浏览量
更新于2024-07-16
收藏 2.4MB PDF 举报
"LINGO教程大全.pdf 是一份详细介绍LINGO软件使用的教程,涵盖了LINGO在数学建模中的应用。LINGO是一款强大的优化求解器,适用于解决非线性规划问题和线性方程组,特别适合处理整数规划,包括0-1整数规划问题。该软件具有内置建模语言,支持多种内建函数,使得建模过程更加灵活,并且能高效地与其他软件如EXCEL和数据库进行数据交换。最新版本为LINGO18.0。"
LINGO教程主要讲解了以下几个方面的知识点:
1. **优化模型的基本概念**:
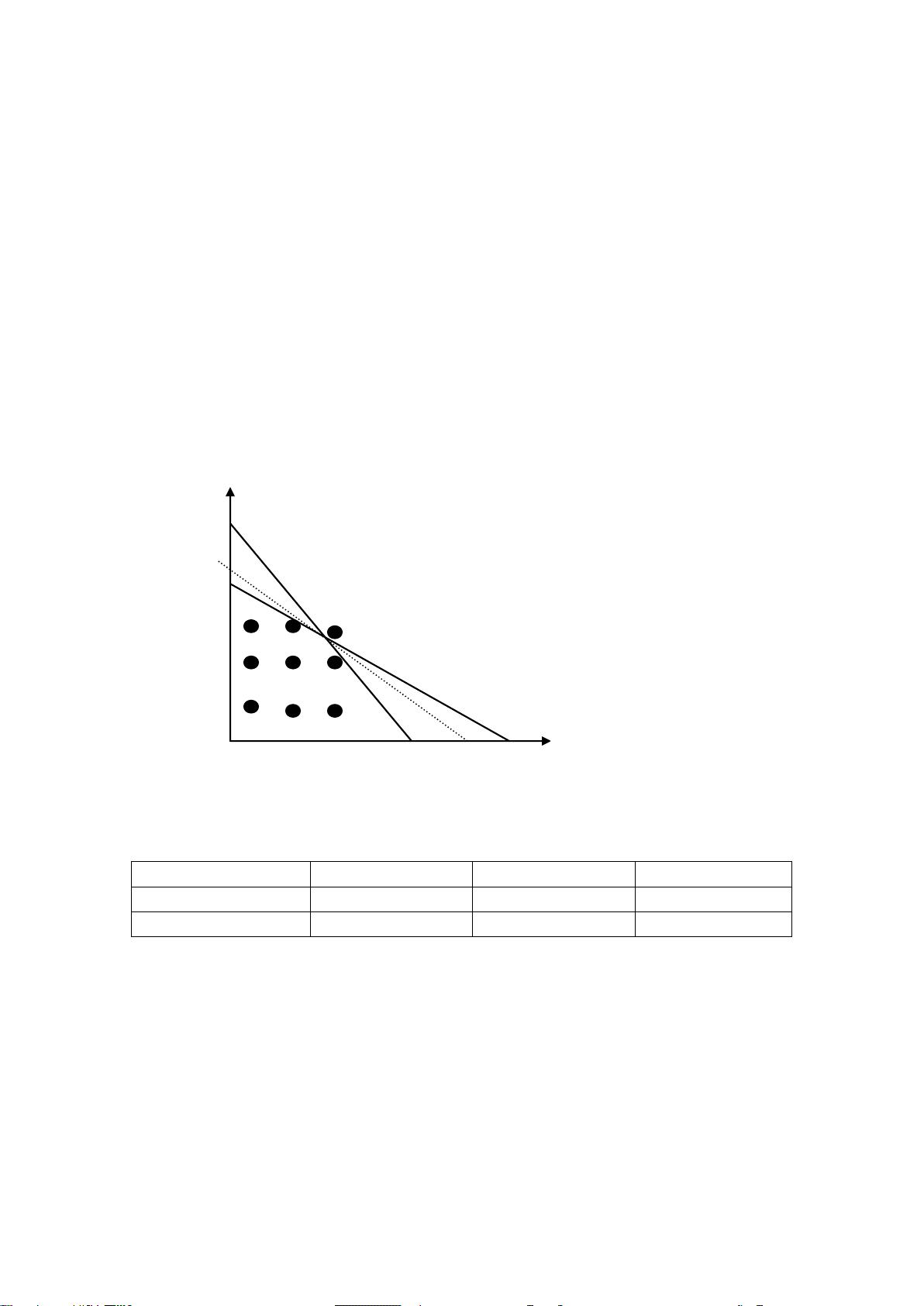
- **优化模型的一般形式**:优化模型通常涉及一个目标函数和一组约束条件。目标函数代表我们要最大化或最小化的量,而约束条件限制了解决方案的空间。
- **可行解与最优解**:可行解是指满足所有约束条件的解,最优解是在可行解集中使目标函数达到最佳值的解。
- **优化模型的基本类型**:主要包括线性规划、二次规划、非线性规划和整数规划。不同类型的模型对应着不同的数学结构和求解策略。
2. **优化问题的建模实例**:
- **线性规划模型**:线性规划是最基础的优化模型,目标函数和约束条件都是线性的。它广泛应用于资源分配、生产计划等领域。
- **二次规划模型**:目标函数为二次函数,约束条件可以是线性的。二次规划常用于处理某些物理或经济问题,如投资组合优化。
- **非线性规划模型**:目标函数或约束条件包含非线性部分,适用于更复杂的问题,如化学工程中的过程设计。
- **整数规划模型**:变量必须取整数值,比连续变量的线性规划更复杂,常见于生产调度、运输问题等。
- **其他优化模型**:还包括混合整数规划、动态规划、随机规划等多种模型,它们分别处理更特殊或更复杂的情况。
LINGO通过其内置的语言和函数库简化了这些模型的构建过程,用户可以方便地定义变量、设定约束和目标函数,然后利用LINGO的强大求解能力找到问题的最优解。此外,与EXCEL等工具的集成使得数据导入导出变得简单,进一步提高了工作效率。
通过学习这个教程,读者将掌握如何利用LINGO来构建和求解各种优化模型,从而在实际问题中实现最优决策,提升业务效率。对于从事运筹学、管理科学、工程优化等领域的专业人士来说,精通LINGO是必不可少的技能之一。
335 浏览量
383 浏览量
318 浏览量
2024-09-08 上传
2024-10-26 上传
161 浏览量
皆非ay
- 粉丝: 27
- 资源: 13
最新资源
- 2009年研究生入学考试计算机统考大纲-完整版.pdf
- MapReduce Simplied Data Processing on Large Clusters.pdf
- 关于usb的驱动开发
- ASP.NET程序设计基础篇
- 数字移相信号发生器设计
- JBoss EJB 3.0 实例教程--企业应用开发核心技术(黎活明)
- LCD液晶显示屏工作原理
- 10秒清除你电脑中的垃圾(使你电脑急速如飞)
- html语法大全,总结了所有的基本语法
- C++Primer4rd 习题解答
- 基于P2P的在线流媒体服务系统
- 一卡通企业应用全面解决方案
- quartz说明文档(适合于java的任务处理)
- DWR中文文档v0.9 欢迎大家下载
- 语音识别区分性训练normandin博士论文
- MyEclipse开发基于 MVC 模式的WEB应用 实例讲解