Java排序算法详解：冒泡、快速、希尔、拓扑、归并

"Java 排序算法的整合教程，涵盖了冒泡、快速、希尔、拓扑和归并排序，提供示例代码以帮助理解和学习排序算法。" 在计算机科学中，排序算法是处理数据的一种重要手段，用于按照特定顺序排列一系列元素。本文将详细介绍Java中的几种常见排序算法，包括冒泡排序、快速排序、希尔排序、拓扑排序和归并排序。 **冒泡排序**是一种简单直观的排序算法，其工作原理就像水底下的气泡一样逐渐上浮。冒泡排序通过比较相邻元素并交换位置来实现排序。在每一轮遍历中，最大的元素会被“冒泡”到数列的末尾。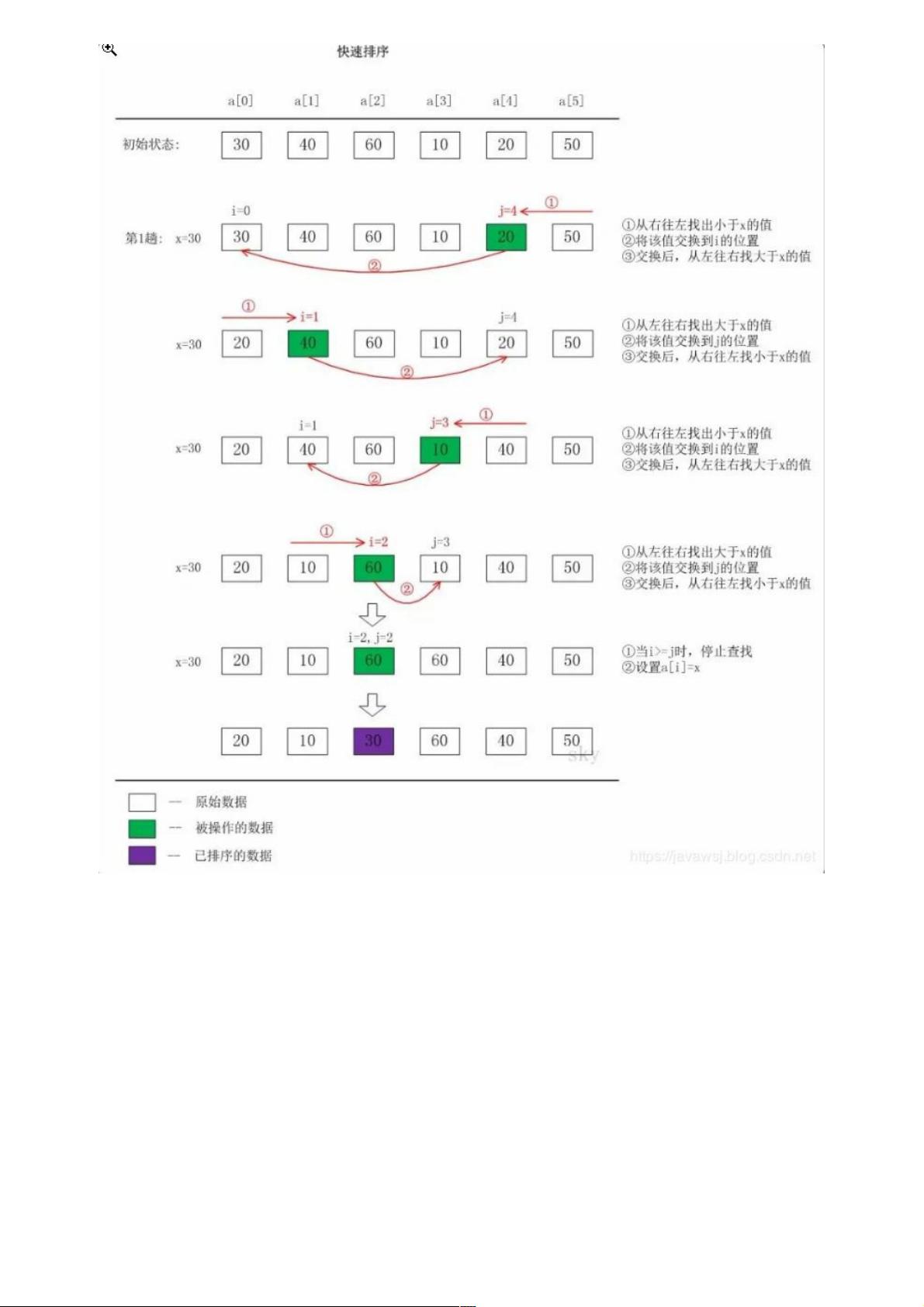以下为Java实现冒泡排序的代码： ```java public static void bubbleSort(int[] a, int n) { int i, j; for (i = n - 1; i > 0; i--) { for (j = 0; j < i; j++) { if (a[j] > a[j + 1]) { // 交换a[j]和a[j+1] int tmp = a[j]; a[j] = a[j + 1]; a[j + 1] = tmp; } } } } ``` **快速排序**是由C.A.R. Hoare提出的，采用分治策略。它选取一个基准元素，通过一趟排序将待排序的数组分为两部分，一部分元素小于基准，另一部分大于基准。然后对这两部分分别进行快速排序。快速排序的平均时间复杂度为O(n log n)。以下是Java实现快速排序的代码： ```java public static void quickSort(int[] a, int l, int r) { if (l < r) { int pivotIndex = partition(a, l, r); quickSort(a, l, pivotIndex - 1); quickSort(a, pivotIndex + 1, r); } } private static int partition(int[] a, int l, int r) { int pivot = a[r]; int i = l - 1; for (int j = l; j < r; j++) { if (a[j] < pivot) { i++; swap(a, i, j); } } swap(a, i + 1, r); return i + 1; } private static void swap(int[] a, int i, int j) { int temp = a[i]; a[i] = a[j]; a[j] = temp; } ``` **希尔排序**是插入排序的一种更高效的改进版本，通过比较相隔一定间隔的元素来减少元素的交换次数。它首先根据某个增量序列对数列进行分组，然后对每个组进行插入排序，最后的增量为1，使得整个数组变得有序。由于希尔排序的具体实现可能有多种，这里不再给出代码示例。 **拓扑排序**通常用于有向无环图(DAG)的排序，它找到一个顶点的入度为0的集合，并将其移除，接着处理剩下的图，直到所有顶点都被移除。拓扑排序并不是对数值的排序，而是对节点的排序。在Java中，可以使用优先队列实现拓扑排序。 **归并排序**是利用分治策略的一种稳定排序算法，它将数组分为两半，分别对这两半进行排序，然后合并两个已排序的半部分。归并排序的时间复杂度为O(n log n)，适用于大规模数据的排序。以下是Java实现归并排序的代码： ```java public static void mergeSort(int[] a, int l, int r) { if (l < r) { int mid = l + (r - l) / 2; mergeSort(a, l, mid); mergeSort(a, mid + 1, r); merge(a, l, mid, r); } } private static void merge(int[] a, int l, int mid, int r) { int n1 = mid - l + 1; int n2 = r - mid; int[] L = new int[n1]; int[] R = new int[n2]; System.arraycopy(a, l, L, 0, n1); System.arraycopy(a, mid + 1, R, 0, n2); int i = 0, j = 0, k = l; while (i < n1 && j < n2) { if (L[i] <= R[j]) { a[k++] = L[i++]; } else { a[k++] = R[j++]; } } while (i < n1) { a[k++] = L[i++]; } while (j < n2) { a[k++] = R[j++]; } } ``` 这些排序算法各有优缺点，适用于不同的场景。例如，冒泡排序简单但效率较低，适合小规模数据；快速排序在大多数情况下表现良好，但最坏情况下时间复杂度为O(n^2)；归并排序和堆排序在任何情况下都能保证O(n log n)的时间复杂度，但需要额外的空间；而希尔排序则在中等规模数据下效率较高。在实际应用中，需要根据具体需求选择合适的排序算法。