Algorithmic Graph Theory - A Comprehensive Introduction

需积分: 9 36 浏览量更新于2024-07-31 收藏 3.05MB PDF 举报

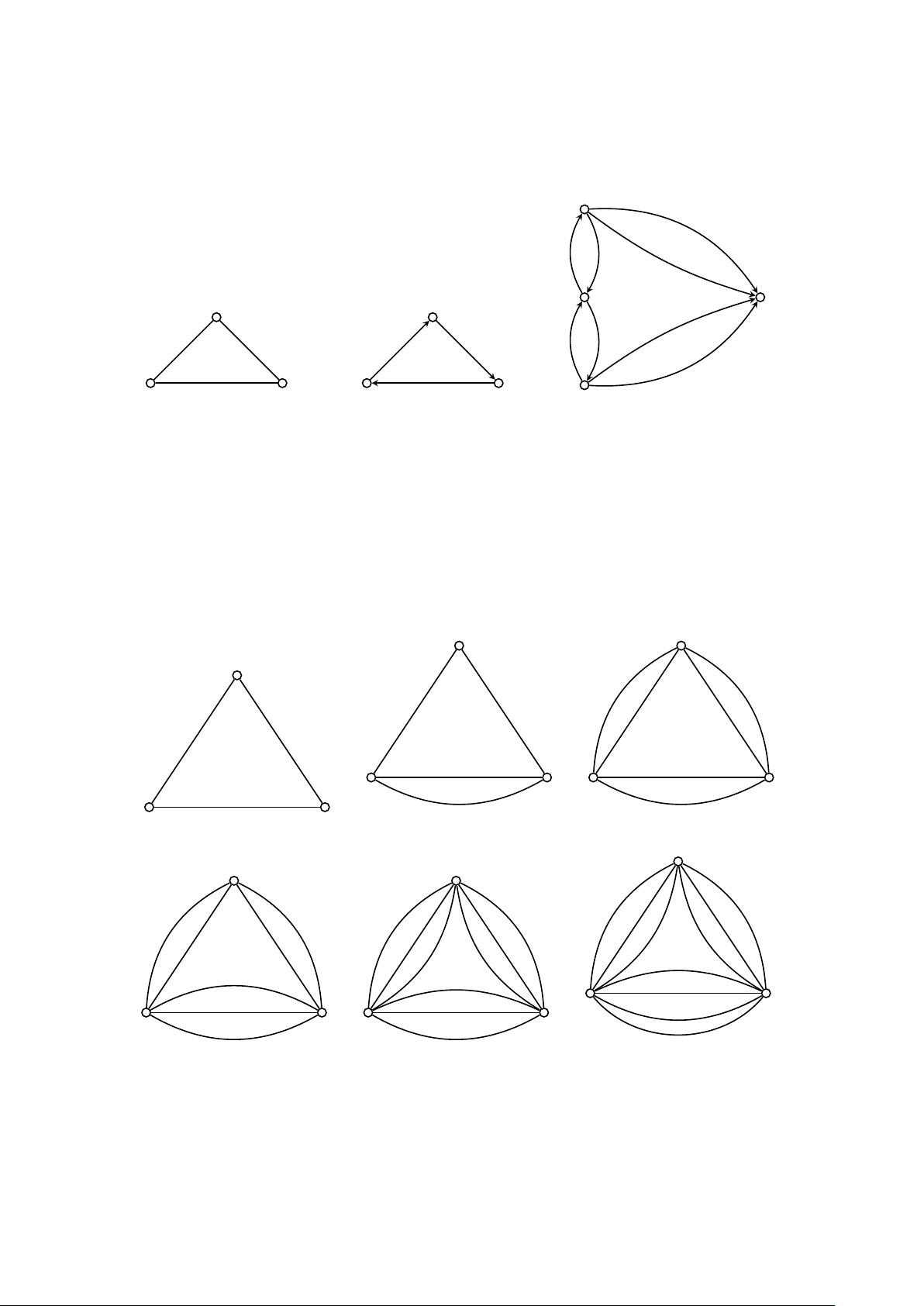
"graph-theory-0.6" 这是一本关于图论的教材，由David Joyner、Minh Van Nguyen和Nathann Cohen合作编写，版本号为0.6。该书涵盖了图论的基础概念和算法，旨在为读者提供深入理解图论的途径。作者们对本书的复制、分发和修改给予了许可，遵循GNU Free Documentation License 1.3或更高版本的条款。在书中，读者可以期待以下内容： 1. **图和有向图** (Graphs and digraphs): 图论的基础是图，它由顶点（vertices）和边（edges）组成。有向图（digraphs）是其中的一种，其边具有方向性，即每个边都有起点和终点。 2. **子图和其他图类型** (Subgraphs and other graph types): 子图是由原图中部分顶点和它们之间的边构成的新图。此外，还有其他特殊类型的图，如树（tree）、平面图（planar graph）、完全图（complete graph）等。 3. **矩阵表示法** (Representing graphs as matrices): 图可以用邻接矩阵或关联矩阵来表示，这是一种用二维数组存储图中顶点间关系的方法。 4. **同构图** (Isomorphic graphs): 同构图是指两个图在结构上是相同的，尽管它们的顶点可能有不同的标记或排列。识别和证明两个图是否同构是图论中的一个重要问题。 5. **新图的构造** (New graphs from old): 通过操作现有图，如并集、笛卡尔积、生成子图等，可以构造出新的图结构。 6. **常见应用** (Common applications): 图论在计算机科学、网络分析、化学、生物学、社会网络等领域有广泛的应用。例如，网络路由、最短路径问题、图的着色问题等。 7. **习题与实例** (Problems and examples): 书中可能包含各种练习题和实际案例，帮助读者巩固理论知识，并将其应用于解决实际问题。这本书是学习和研究图论的理想资源，适合计算机科学、数学专业的学生以及对图论感兴趣的读者。由于它是开源的，读者可以访问提供的网站获取最新版本和更多资源。

4 Chapter 1. Introduction to Graph Theory

sage : G = Graph ({ "a " :[ " b " ," e "], "b":[ "a" ,"c " ,"e " ], " c":[ "b" ,"d"] ,

... "d" :[ "c" ,"e " ], " e":[ "a" ,"b","d" ]})

sage : G

Graph on 5 vertices

sage : G. vertices ()

[ ’a ’, ’b’, ’c ’, ’d’, ’e’]

sage : G. edges ( labels = False )

[( ’a ’, ’b ’) , ( ’a ’ , ’e ’) , ( ’b ’ , ’e ’), ( ’c’, ’b ’) , ( ’c ’, ’d’), ( ’e ’, ’d ’)]

The graph G is undirected, meaning that we do not impose direction on any edges.

Without any direction on the edges, the edge ab is the same as the edge ba. That is why

G.edges() returns six edges instead of the 12 edges listed in (1.1).

(2) Let adj(v) be the set of all vertices that are adjacent to v. Then we have

adj(a) = {b, e}

adj(b) = {a, c, e}

adj(c) = {b, d}

adj(d) = {c, e}

adj(e) = {a, b, d}.

The vertices adjacent to v are also referred to as its neighbors. We can use the function

G.neighbors() to list all the neighbors of each vertex.

sage : G. neigh bo rs ( "a")

[ ’b ’, ’e’]

sage : G. neigh bo rs ( "b")

[ ’a ’, ’c’, ’e ’]

sage : G. neigh bo rs ( "c")

[ ’b ’, ’d’]

sage : G. neigh bo rs ( "d")

[ ’c ’, ’e’]

sage : G. neigh bo rs ( "e")

[ ’a ’, ’b’, ’d ’]

(3) Taking the cardinalities of the above ﬁve sets, we get |adj(a)| = |adj(c)| =

of adjacent vertices, while b and e have the largest number of adjacent vertices.

(4) If all the edges in G are removed, the result is still a graph, although one without

any edges. By deﬁnition, the edge set of any graph is a subset of V

(2)

. Removing all

edges of G leaves us with the empty set ∅, which is a subset of every set.

(5) Say we remove all of the vertices from the graph in Figure 1.3 and in the process

all edges are removed as well. The result is that both of the vertex and edge sets are

empty. This is a special graph known as the empty or null graph.

Example 1.3. Consider the illustration in Figure 1.4. Does Figure 1.4 represent a

graph? Why or why not?

Solution. If V = {a, b, c} and E = {aa, bc}, it is clear that E ⊆ V

(2)

. Then (V, E) is a

graph. The edge aa is called a self-loop of the graph. In general, any edge of the form

vv is a self-loop.

In Figure 1.3, the edges ae and ea represent one and the same edge. If we do not

consider the direction of the edges in the graph of Figure 1.3, then the graph has six

edges. However, if the direction of each edge is taken into account, then there are 12 edges

as listed in (1.1). The following deﬁnition captures the situation where the direction of

the edges are taken into account.

A directed edge is an edge such that one vertex incident with it is designated as

the head vertex and the other incident vertex is designated as the tail vertex. In this

1.1. Graphs and digraphs 5

Figure 1.4: A ﬁgure with a self-loop.

situation, we may assume that the set of edges is a subset of the ordered pairs V × V .

A directed edge uv is said to be directed from its tail u to its head v. A directed graph

or digraph G is a graph each of whose edges is directed. The indegree id(v) of a vertex

v ∈ V (G) counts the number of edges such that v is the head of those edges. The

outdegree od(v) of a vertex v ∈ V (G) is the number of edges such that v is the tail of

those edges. The degree deg(v) of a vertex v of a digraph is the sum of the indegree and

the outdegree of v.

Let G be a graph without self-loops and multiple edges. It is important to distinguish

a graph G as being directed or undirected. If G is undirected and uv ∈ E(G), then uv

and vu represent the same edge. In case G is a digraph, then uv and vu are diﬀerent

directed edges. For a digraph G = (V, E) and a vertex v ∈ V , all the neighbors of v

in G are contained in adj(v), i.e. the set of all neighbors of v. Just as we distinguish

between indegree and outdegree for a vertex in a digraph, we also distinguish between in-

neighbors and out-neighbors. The set of in-neighbors iadj(v) ⊆ adj(v) of v ∈ V consists

of all those vertices that contribute to the indegree of v. Similarly, the set of out-neighbors

oadj(v) ⊆ adj(v) of v ∈ V are those vertices that contribute to the outdegree of v. Then

iadj(v) ∩ oadj(v) = {u | uv ∈ E and vu ∈ E}

and adj(v) = iadj(v) ∪ oadj(v).

1.1.1 Multigraphs

This subsection presents a larger class of graphs. For simplicity of presentation, in this

book we shall assume usually that a graph is not a multigraph. In other words, when you

read a property of graphs later in the book, it will be assumed (unless stated explicitly

otherwise) that the graph is not a multigraph. However, as multigraphs and weighted

graphs are very important in many applications, we will try to keep them in the back

of our mind. When appropriate, we will add as a remark how an interesting property of

“ordinary” graphs extends to the multigraph or weighted graph case.

An important class of graphs consist of those graphs having multiple edges between

pairs of vertices. A multigraph is a graph in which there are multiple edges between a

pair of vertices. A multi-undirected graph is a multigraph that is undirected. Similarly,

a multidigraph is a directed multigraph.

As we indicated above, a graph may have “weighted” edges.

Deﬁnition 1.4. A weighted graph is a graph G = (V, E) where each set V and E is a

pair consisting of a vertex and a real number called the weight.

The illustration in Figure 1.1 is actually a multigraph, a graph with multiple edges,

called the K¨onigsberg graph.

1.1. Graphs and digraphs 7

The unweighted degree deg(v) of a vertex v of a weighted multigraph is the sum of the

unweighted indegree and the unweighted outdegree of v:

deg(v) = deg

(v) + deg

−

(v).

Loops are counted twice.

Similarly, there is the set of in-neighbors

iadj(v) = {w ∈ V | for some e ∈ E, i(e) = {v, w}, h(e) = v}

and the set of out-neighbors

oadj(v) = {w ∈ V | for some e ∈ E, i(e) = {v, w}, h(e) = w}.

Deﬁne the adjacency of v to be the union of these:

adj(v) = iadj(v) ∪ oadj(v).

It is clear that deg

(v) = | iadj(v)| and deg

−

(v) = | oadj(v)|.

The weighted indegree of a vertex v ∈ V counts the weights of edges going into v:

wdeg

(v) =

e∈E

h(e)=v

The weighted outdegree of a vertex v ∈ V counts the weights of edges going out of v:

wdeg

−

(v) =

e∈E

v∈i(e)={v,v

}

h(e)=v

The weighted degree of a vertex of a weighted multigraph is the sum of the weighted

indegree and the weighted outdegree of that vertex. In other words, it is the sum of

the weights of the edges incident to that vertex, regarding the graph as an undirected

weighted graph.

1.1.2 Simple graphs

A simple graph is a graph with no self-loops and no multiple edges. Figure 1.6 illustrates

a simple graph and its digraph version, together with a multidigraph version of the

K¨onigsberg graph. The edges of a digraph can be visually represented as directed arrows,

similar to the digraph in Figure 1.6(b) and the multidigraph in Figure 1.6(c). The digraph

in Figure 1.6(b) has the vertex set {a, b, c} and the edge set {ab, bc, ca}. There is an arrow

from vertex a to vertex b, hence ab is in the edge set. However, there is no arrow from

b to a, so ba is not in the edge set of the graph in Figure 1.6(b). The family Sh(n) of

Shannon multigraphs is illustrated in Figure 1.7 for integers 2 ≤ n ≤ 7. These graphs

are named after Claude E. Shannon (1916–2001). Each Shannon multigraph consists of

three vertices, giving rise to a total of three distinct unordered pairs. Two of these pairs

are connected by bn/2c edges and the third pair of vertices is connected by b(n + 1)/2c

edges.

剩余247页未读，继续阅读

mxf3306

粉丝: 2
资源: 3

Algorithmic Graph Theory - A Comprehensive Introduction

Graph-Transformer在图形分类中的应用与Pytorch/Tensorflow实现

Graph-Bert源代码解读：Python图形表示学习框架

Graph-RAT-开源软件：数据库图形分析利器

图论课件--最短路算法与代数表示详解

Python库graph-notebook新版本发布

基于微信小程序的社区门诊管理系统php.zip

白色大气风格的设计师作品模板下载.zip

工程经济学自考必备软件下载

UML课程设计报告.doc

白色大气风格响应式彩绘精品水果网站模板.zip

最新资源