逻辑回归详解:目标、方法与应用实例
需积分: 0 5 浏览量
更新于2024-06-30
收藏 1.72MB PDF 举报
第三讲是关于机器学习中的逻辑回归,它是统计学习理论中一种用于预测二分类问题的算法。在这一讲中,主要学习目标包括:
1. 线性回归基础:首先回顾线性回归,这是一种基本的预测模型,它假设因变量和自变量之间存在线性关系。线性回归模型通过回归系数(𝛽𝛽0, 𝛽𝛽1, ..., 𝛽𝛽𝐷𝐷)来表达这种关系,其形式为 \( y_i = \beta_0 + \beta_1 x_{i1} + ... + \beta_D x_{iD} \),其中\( x_{ij} \)是特征值,\( i \)表示样本索引,\( D \)是特征维度。
2. 贝叶斯线性回归:在这个部分,介绍了贝叶斯方法对线性回归的处理,即考虑了先验知识对模型参数的影响,使得模型更加灵活和不确定性量化。
3. 逻辑回归介绍:逻辑回归是专为分类任务设计的,特别是二分类问题,将连续的输出映射到0和1的概率。不同于线性回归,逻辑回归的输出经过sigmoid函数转换,确保结果在0到1之间,代表正类的概率。
4. 模型求解方法:逻辑回归通常使用最大似然估计或梯度下降法等优化算法求解模型参数,确保模型能够最小化交叉熵损失函数。
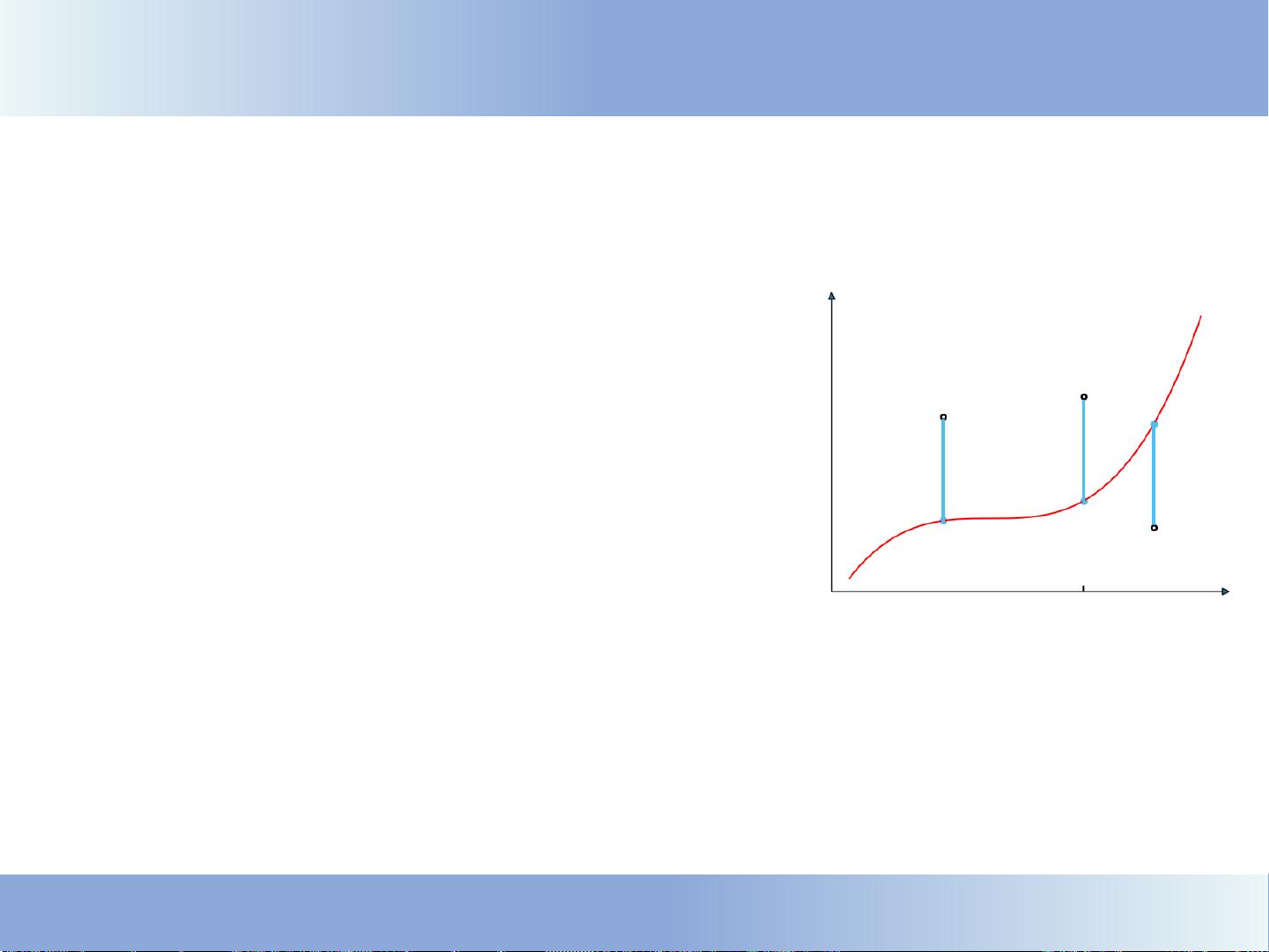
5. 基函数和非线性特征:逻辑回归通过使用多项式基函数和高斯核函数(如径向基函数RBF)等非线性转换,使得模型能够拟合非线性关系。这样即使原始特征是线性的,通过适当的特征转换,逻辑回归也能捕捉到复杂的关系。
6. 实际应用示例:以大熊猫食量数据为例,展示了如何使用逻辑回归来建立模型,通过分析不同月份的食量数据,预测个体的大熊猫食性或行为特征。
7. 课程结构:该讲义还包括了课程大纲,依次讲解了线性回归、贝叶斯线性回归、逻辑回归以及贝叶斯逻辑回归,让学习者逐步深入理解这些概念和技术。
通过学习这第三讲,学员将能够理解和掌握逻辑回归的基本原理、模型构建和应用,这对于数据挖掘和机器学习初学者来说是一个重要的基础知识点。
127 浏览量
193 浏览量
点击了解资源详情
2022-08-04 上传
155 浏览量
206 浏览量
296 浏览量
483 浏览量
chenbtravel
- 粉丝: 28
最新资源
- Premiere Pro CS6视频编辑项目教程微课版教案
- SSM+Lucene+Redis搜索引擎缓存实例解析
- 全栈打字稿应用:演示项目实践与探索
- 仿Windows风格的AJAX无限级树形菜单实现教程
- 乐华2025L驱动板通用升级解决方案
- Java通过jcraft实现SFTP文件上传下载教程
- TTT素材-制造1资源包介绍与记录
- 深入C语言编程技巧与实践指南
- Oracle数据自动导出并转换为Excel工具使用教程
- Ubuntu下Deepin-Wine容器的使用与管理
- C语言网络聊天室功能详解:禁言、踢人与群聊
- AndriodSituationClick事件:详解按钮点击响应机制
- 探索Android-NetworkCue库:高效的网络监听解决方案
- 电子通信毕业设计:简易电感线圈制作方法
- 兼容性数据库Compat DB 4.2.52-5.1版本发布
- Android平台部署GNU Linux的新方案:dogeland体验