数据拟合与Romberg求积法的计算机实现

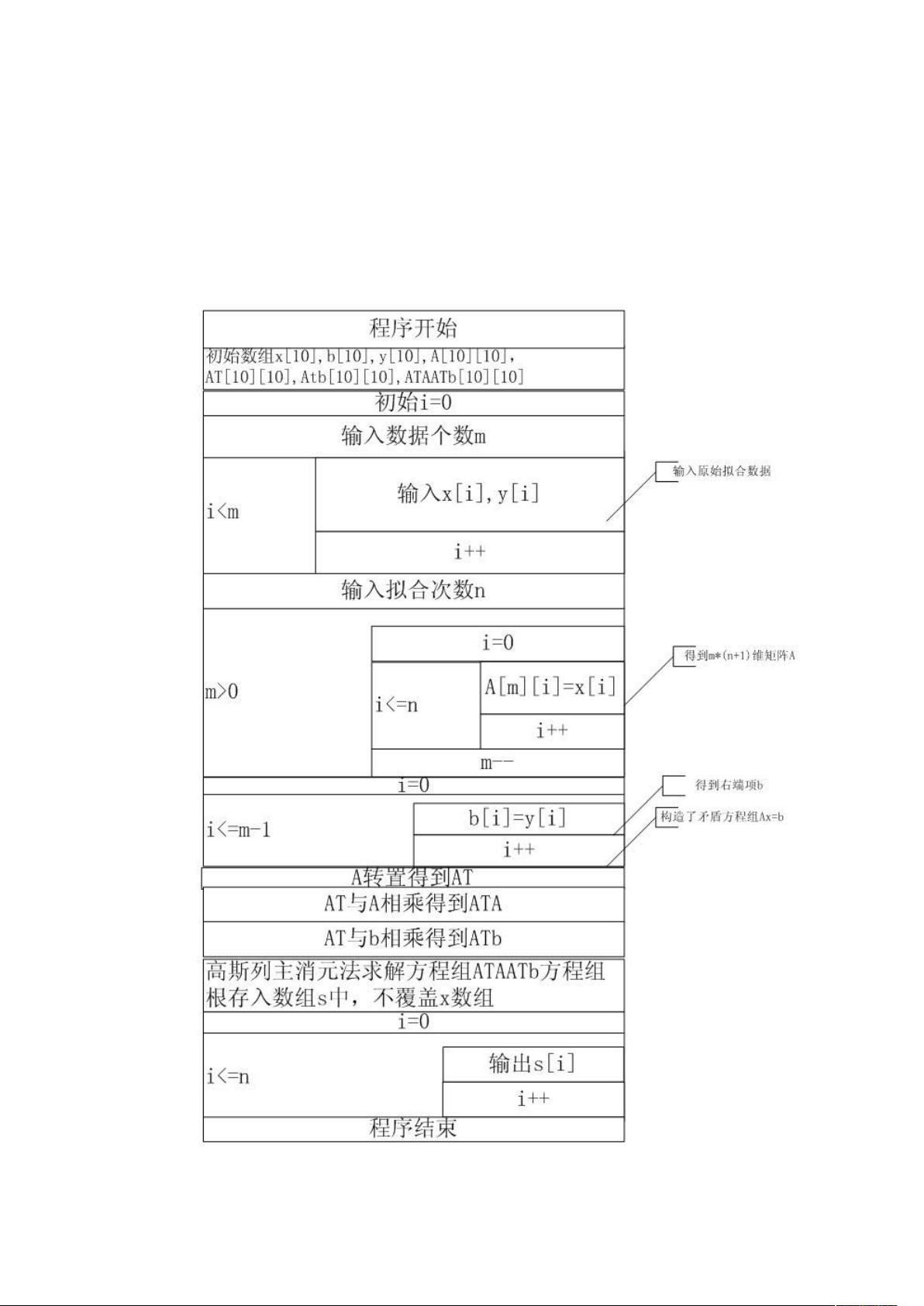
"该实验是关于计算机数值方法的实践，主要涉及数据拟合的最小二乘法和Romberg求积法。实验目的是通过给定的数据点，利用计算机找到最佳拟合曲线，即多项式或幂级数。实验内容包括手动输入数据或文件输入数据，然后进行多项式拟合或幂级数拟合，并输出拟合结果。通过算例展示了不同拟合方式和次数的输出，以验证算法的正确性。" 在计算机数值方法中，数据拟合的最小二乘法是一种常见的技术，用于寻找一条最佳拟合曲线，使得所有数据点到这条曲线的垂直距离平方和最小。这种技术广泛应用于各种科学和工程问题，如数据分析、模型构建等。在本实验中，最小二乘法被用于多项式拟合，通过给定的坐标点(x, y)，找到一个多项式函数P(x) = c0 + c1*x + c2*x^2 + ... + cn*x^n，其中ci是待求的系数，n是拟合次数。最小二乘法的基本思想是通过最小化残差平方和来确定这些系数，即最小化 ∑(yi - P(xi))^2。 实验中，用户可以选择手动输入数据，输入包含点的坐标和拟合次数，或者选择文件输入，程序会自动处理数据。输出结果不仅包括拟合的多项式函数形式，还展示了计算过程和拟合的坐标点，这有助于理解和验证拟合效果。 此外，实验还提到了Romberg求积法，这是一种高精度的数值积分方法。它基于梯形法则，通过重复应用梯形规则并在不同间隔上进行外推，可以提高积分的精度。Romberg方法适用于对精确积分值有较高要求的情况，特别是在数据量较大或者被积函数复杂时，能够提供比简单矩形法或梯形法更好的精度。 部分源程序中，精度要求定义为#define eps 0.000005，这表明在求解过程中将使用这个精度作为判断解是否收敛的标准。同时，使用了矩阵结构体来存储数据，便于进行线性代数运算，如求解系数矩阵的逆矩阵，这是实现最小二乘法的关键步骤。矩阵结构体包含了一个二维浮点数数组和行数信息，方便进行矩阵运算。 这个实验涵盖了数值分析中的基础概念和实际应用，对于理解数据拟合和数值积分方法有着重要的实践价值。通过实际操作，学生可以深入理解这些方法的原理并掌握其使用技巧。