笛卡尔积图的完美性探究

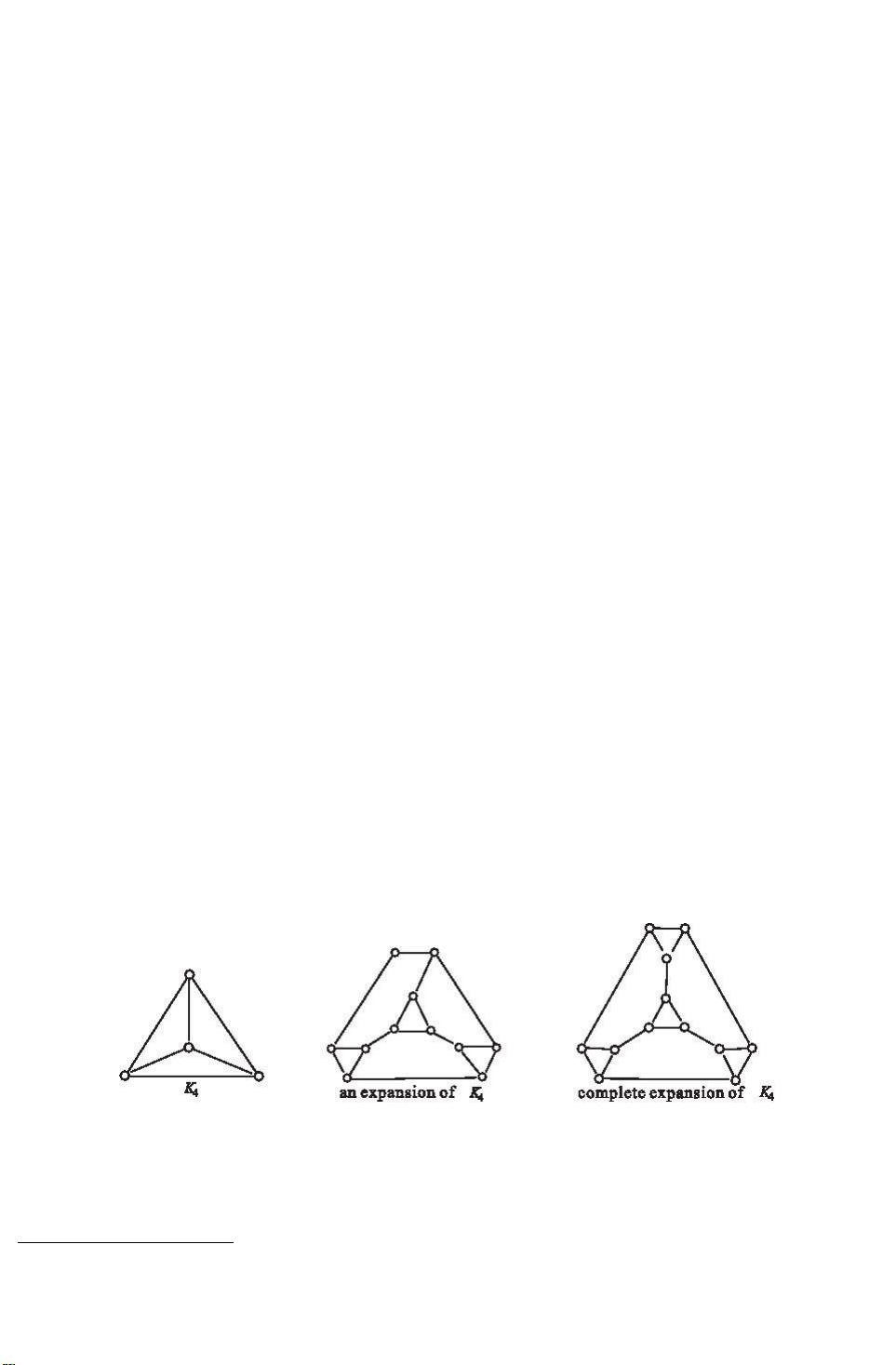
"本文主要探讨了图的笛卡尔积图的结构以及其完美性的理论。作者通过研究笛卡尔积这一图论操作，揭示了扩容图的特性，并且得出了与线图的笛卡尔积之间的联系。文章指出，完全扩容图具有完美的性质。" 在图论中，笛卡尔积是一种构造新图的方法，它将两个图G和H的顶点集进行笛卡尔积，然后连接每对顶点(u, v)和(w, x)，如果u和w在G中是相邻的，或者v和x在H中是相邻的。这种操作可以产生复杂的图结构，为研究图的性质提供了新的视角。在本文中，作者Siqin和阿勇嘎关注的是这种构造对于图的完美性的影响。 完美图是图论中的一个重要概念，一个图被称为完美，如果它的每一个诱导子图的 chromatic数等于其最大团的大小。这里的chromatic数指的是将图的顶点着色，使得相邻的顶点颜色不同所需的最少颜色数，而最大团是图中最大的完全子图。完美图的研究在组合优化、编码理论等领域有广泛的应用。 作者利用笛卡尔积来描述扩容图，这是一种通过添加新的边来扩展原图的方法。扩容通常会改变原图的结构，但保持某些特性不变。在文中，他们证明了扩容图与原图的线图的笛卡尔积之间存在密切的关系，线图是将原图的每一条边替换为一个团（即完全图），其中团的顶点代表原边的端点。 通过深入分析，作者得出结论，当扩容图是完全扩容时，即每个顶点都与其他所有顶点相连，这样的图是完美的。这意味着完全扩容图的所有诱导子图的chromatic数都等于其最大团的大小，这是一个重要的理论发现，对理解图的结构性质和算法设计有深远意义。 此外，文章还引用了相关的数学分类代码和文献检索代码，表明这是在学术界发表的研究成果，具有一定的学术价值。通过这些代码，读者可以进一步追踪该领域的其他相关研究，深化对图论的理解。 这篇文章深入探讨了图的笛卡尔积和扩容图的完美性问题，为图论研究提供了新的理论基础，对于理解复杂网络的结构和性质，尤其是在计算复杂性和图的染色问题上，具有重要的理论和实际意义。