高级数据结构：平衡二叉树与AVL树解析

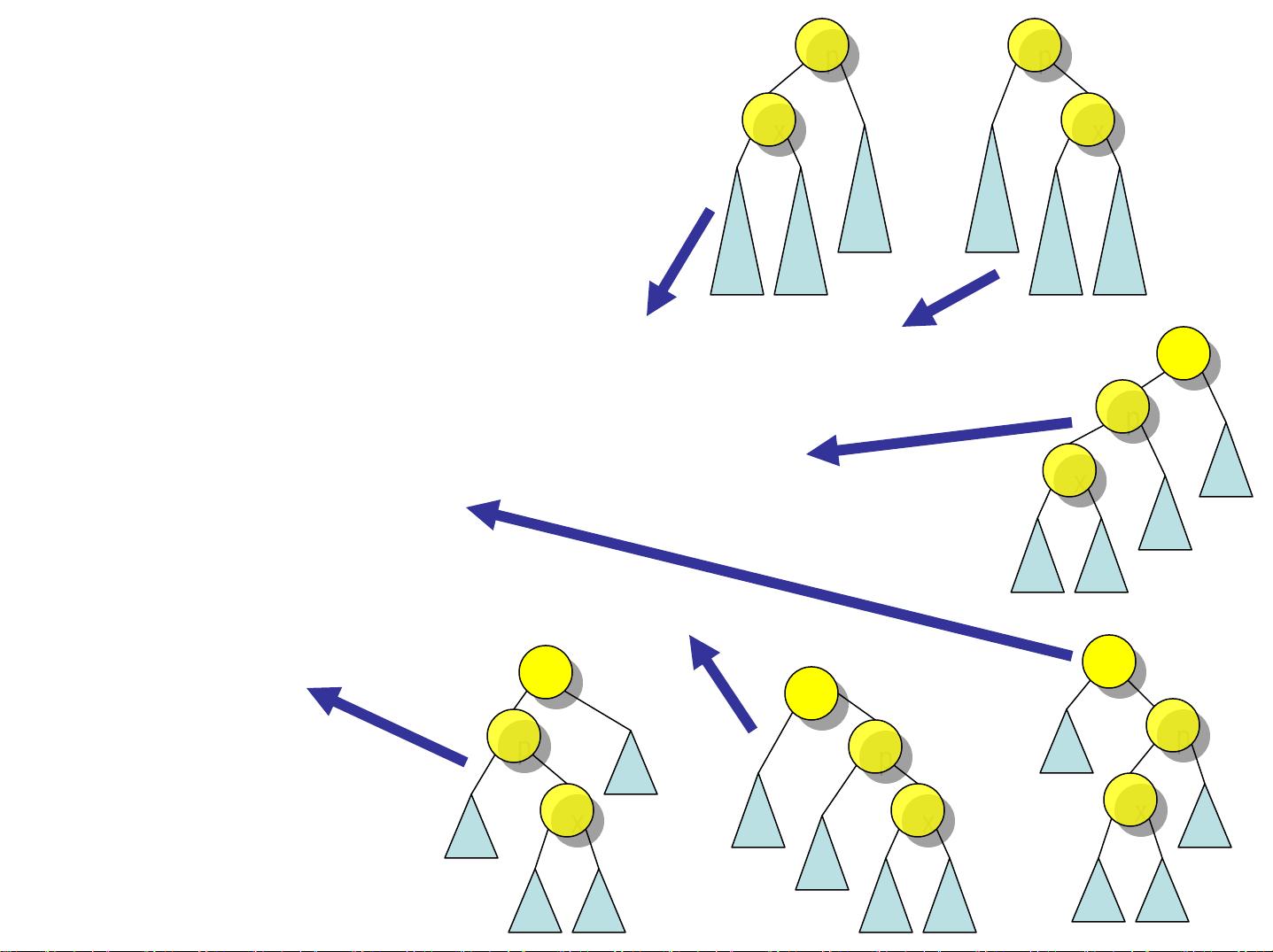
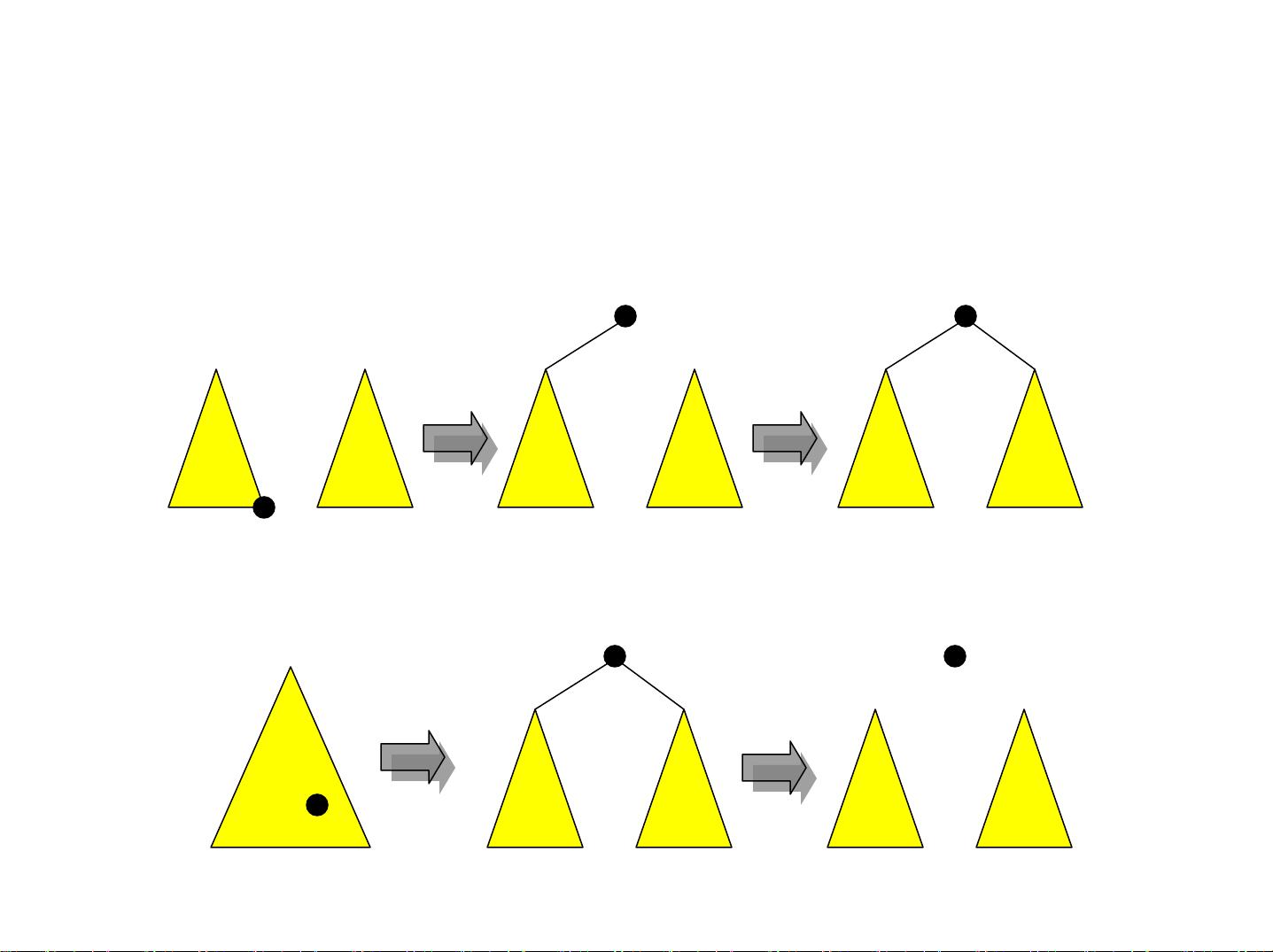
"高级数据结构课程讲解，包括平衡二叉树、可并优先队列、线段树和树状数组基础、RMQ与LCA等主题。由刘汝佳讲解，重点介绍了AVL树的平衡性质和旋转操作，以及如何在插入过程中保持平衡。" 在计算机科学中，高级数据结构是构建复杂算法和高效解决方案的关键工具。本课程着重讲解了一些重要的高级数据结构，如平衡二叉树，这对于理解高效搜索和操作具有重要意义。 首先，基本BST（Binary Search Tree，二叉搜索树）是一种特殊的二叉树，其中每个节点的左子树上的所有节点值都小于该节点，而右子树上的节点值都大于该节点。查找、插入和删除操作的时间复杂度取决于树的高度。理想情况下，如果树是平衡的，那么高度为O(logn)，但如果不平衡，高度可能会达到O(n)，导致性能下降。 平衡二叉树，如AVL树，是为了确保树保持相对平衡，从而提高操作效率。AVL树的定义是，任何节点的两个子树高度差不超过1。通过引入旋转操作，即单旋转和双旋转，AVL树可以在插入或删除操作后重新平衡自身。例如，当右子树过高时，可以进行右旋操作；当左子树过高时，先左旋再右旋。这些旋转操作可以确保树的高度始终保持在O(logn)级别。 插入算法在AVL树中的应用需要从插入的元素向上遍历到第一个不平衡的节点，然后进行相应的旋转操作来恢复平衡。这一过程涉及到祖父节点、父节点和子节点之间的关系分析，根据它们的相对位置决定执行单旋转还是双旋转。 此外，课程还涵盖了可并优先队列、线段树和树状数组，这些都是解决范围查询和最值问题的有效数据结构。RMQ（Range Minimum/Maximum Query）用于找到给定区间内的最小/最大值，而LCA（Lowest Common Ancestor）则寻找两个节点在树中的最近公共祖先。 这门课程深入探讨了高级数据结构的概念和实现，对于提升算法设计和复杂问题解决能力非常有帮助。通过学习这些内容，开发者能够更好地理解和使用这些高级数据结构，优化他们的代码，提高软件的性能。