"基于Matlab的Lorenz系统混沌仿真研究"
DOC格式 | 791KB |
更新于2023-12-23
| 144 浏览量 | 举报
本研究基于matlab对Lorenz系统进行了深入的仿真研究。首先,通过对Lorenz方程的分析和求解,利用matlab绘制了Lorenz混沌吸引子的三维图形,并对Lorenz混沌系统的初值敏感性进行了直观观测。其次,我们对Lorenz系统进行了仿真,比较分析在不同参数下系统的仿真结果,进一步揭示了Lorenz系统的特性和行为。最后,我们通过添加反馈控制方式,验证了可以使Lorenz方程不稳定平衡点成为稳定平衡点的结论。这些研究成果为我们更深入地理解Lorenz系统的特性和行为提供了重要的实验数据和分析结果。此外,Lorenz方程作为混沌领域的典型方程,对于气候变化和对流实验等方面有着重要的应用意义。因此,本研究对于深入理解Lorenz系统的行为规律,以及对混沌动力系统的研究具有一定的理论和应用价值。
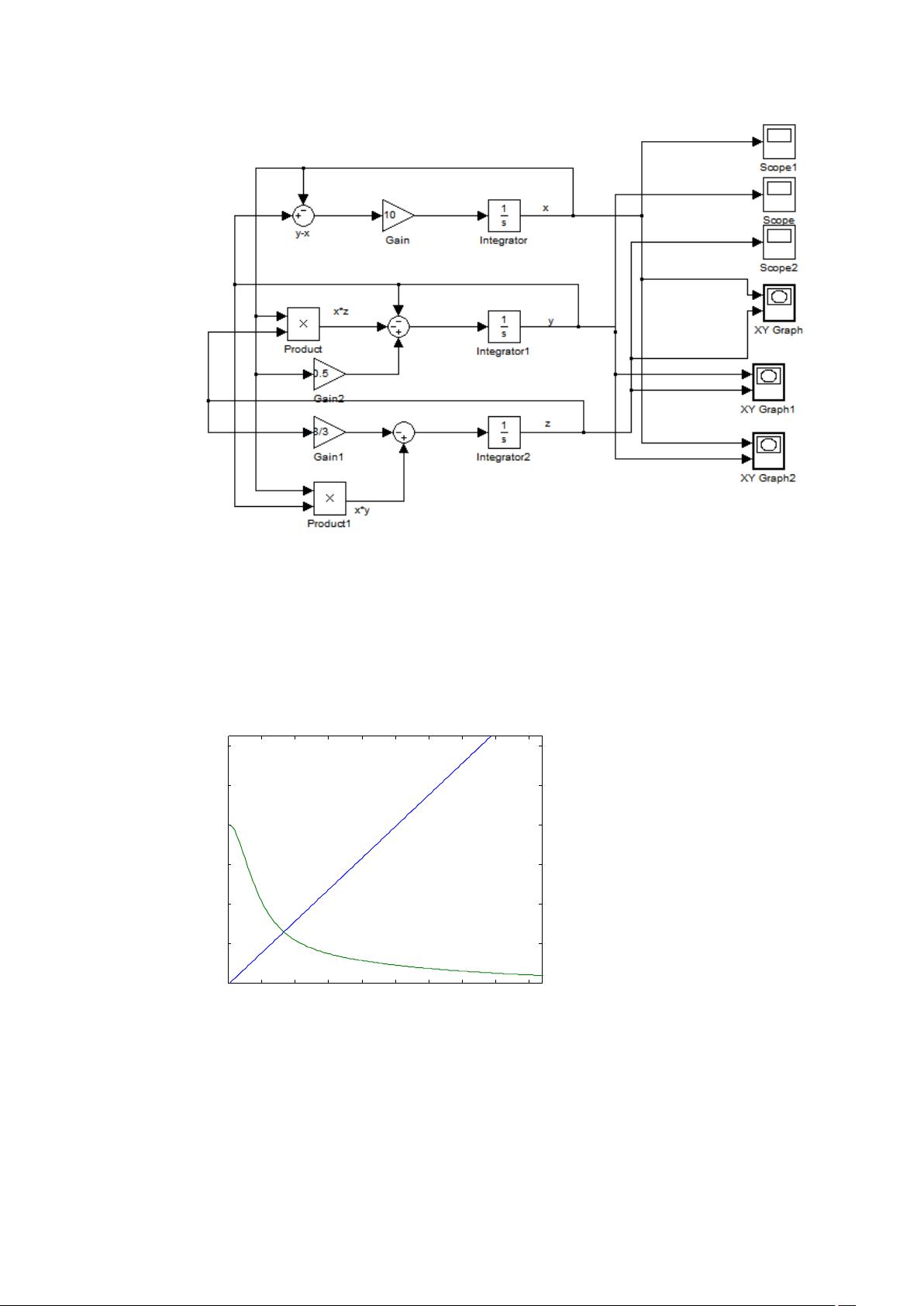
Lorenz方程是由美国著名气象学家Lorenz在1963年为研究气候变化而建立的,是混沌领域典型的方程之一。本文通过使用matlab这一强大的数学工具,对Lorenz系统进行了详细的研究和分析。首先,我们使用matlab求解了Lorenz方程,并利用其绘图功能绘制了Lorenz混沌吸引子的三维图形,直观展示了Lorenz系统的混沌特性和吸引子的形态。同时,我们对Lorenz系统的初值敏感性进行了简单观测,进一步加深了对系统行为的理解。接着,我们进行了系统的仿真研究,比较了在不同参数下的系统仿真成果,发现不同参数下系统呈现出不同的行为特征,这为进一步研究系统行为提供了重要的数据支持。最后,我们验证了通过添加反馈控制方式,可以将Lorenz方程的不稳定平衡点转变为稳定平衡点,这为对系统行为的控制和调节提供了一个实用的方法。
本研究通过对Lorenz系统的深入研究,为了解混沌动力系统的特性和规律提供了重要的实验数据和分析结果。Lorenz方程在气候变化和对流实验等领域有着重要的应用价值,因此对于其行为规律的深入理解具有一定的理论和实际意义。同时,通过使用matlab这一数学工具,我们能够更直观地展示系统的混沌特性和行为,为进一步研究和探索混沌动力系统提供了一个重要的研究方法和工具。总之,本研究对于Lorenz系统的研究和对混沌动力系统的理解具有一定的理论和实际意义。
相关推荐







智慧安全方案
- 粉丝: 3857
最新资源
- 自动生成CAD模型文件的测试流程
- 掌握JavaScript中的while循环语句
- 宜科高分辨率编码器产品手册解析
- 探索3CDaemon:FTP与TFTP的高效传输解决方案
- 高效文件对比系统:快速定位文件差异
- JavaScript密码生成器的设计与实现
- 比特彗星1.45稳定版发布:低资源占用的BT下载工具
- OpenGL光源与材质实现教程
- Tablesorter 2.0:增强表格用户体验的分页与内容筛选插件
- 设计开发者的色值图谱指南
- UYA-Grupo_8研讨会:在DCU上的培训
- 新唐NUC100芯片下载程序源代码发布
- 厂家惠新版QQ空间访客提取器v1.5发布:轻松获取访客数据
- 《Windows核心编程(第五版)》配套源码解析
- RAIDReconstructor:阵列重组与数据恢复专家
- Amargos项目网站构建与开发指南