GPS高程拟合：二次曲面法与多面函数法比较

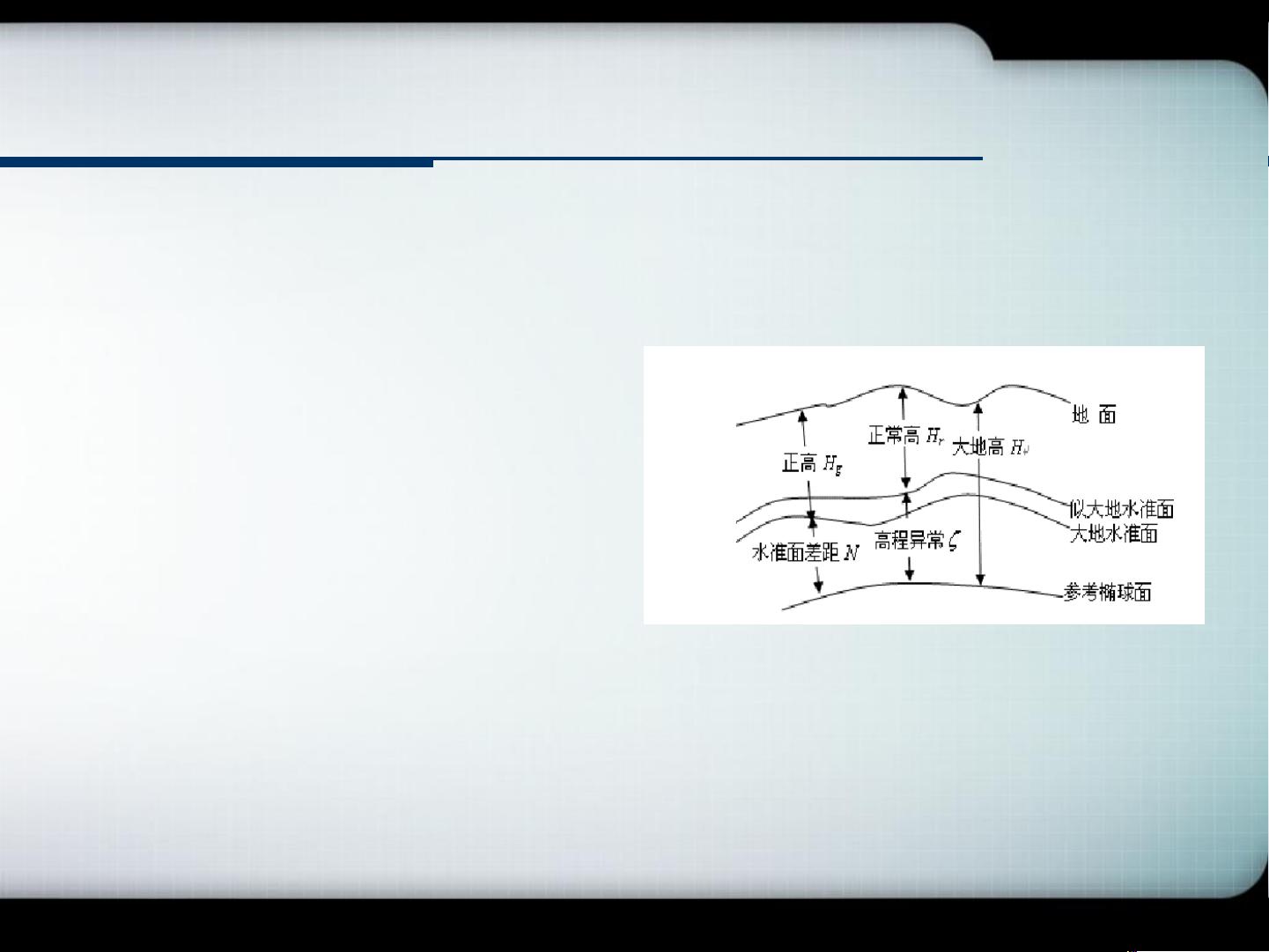
"该资源是一份关于多面函数与二次曲面高程拟合精度比较的教学课件，由张晖于2012年12月3日制作。内容涉及GPS高程拟合的基本理论、二次曲面法和多面函数法的拟合方法，并通过实例分析和总结进行了详细讲解。" 在测绘领域，GPS平面测量数据因其高精度而被广泛应用。然而，如何将这些数据转换为可用于实际应用的正常高是个关键问题。GPS高程拟合就是解决这一问题的重要手段，主要是通过计算高程异常来转换大地高为正常高。正常高是以大地水准面为基准的高程系统，而大地高则是基于参考椭球面的高程系统。由于这两者不重合，因此存在高程异常，即\( \gamma \)。 二次曲面法是一种常见的高程拟合方法，它基于多项式曲面拟合的模型，通常采用3次或更低次幂的多项式，例如二次多项式，公式可表示为： \[ \gamma = a_0 + a_1x + a_2y + a_3xy + a_4x^2 + a_5y^2 + a_6x^2y + a_7xy^2 + a_8y^3 + a_9x^3 \] 这里，\( a_i \)是待定参数，通过已知点的平面坐标\( x, y \)（或大地坐标\( B, L \)）和高程异常值来确定。构建一个包含所有已知点的方程组矩阵，然后解这个线性系统，就能得到这些参数，进一步计算出未知点的高程异常\( \gamma \)，从而得到正常高\( H \)。 多面函数法是另一种拟合方法，它可能适用于点位成面状分布的情况，通常会比二次曲面法更为复杂，但可能会提供更好的拟合效果。这种方法可能包括使用多个曲面来更精确地描述地形的变化，适合处理复杂的地表形态。 实例分析部分会通过具体的案例展示这两种方法在实际操作中的表现，包括它们的拟合精度和计算复杂度。总结分析则会综合评价两种方法的优缺点，给出适用场景的建议。 这份课件旨在探讨在GPS点位分布特定情况下，二次曲面法和多面函数法在高程拟合中的适用性和精度差异，对于理解高程转换和选择合适的拟合方法具有指导意义。