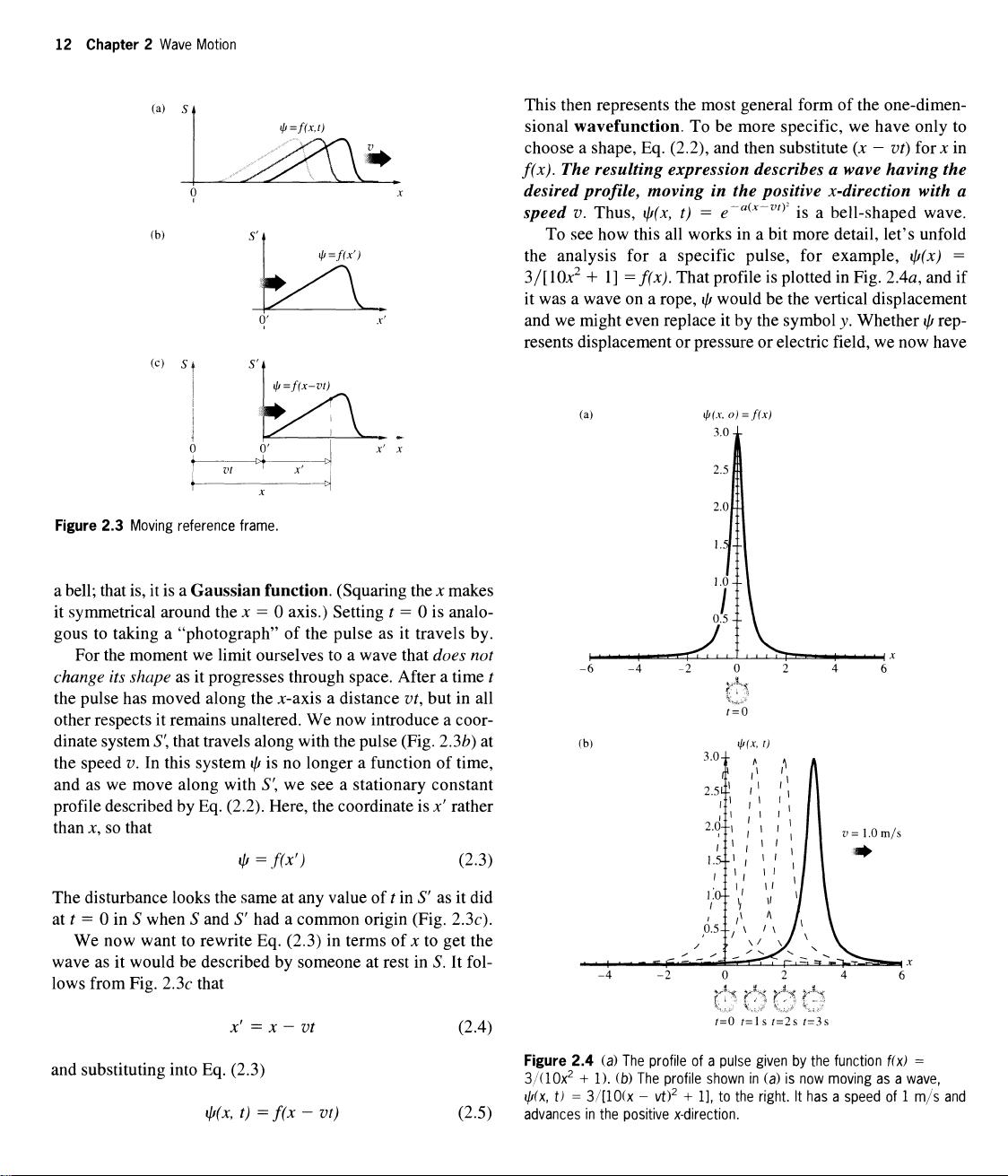
2.1 One-Dimensional Waves 13
the profile of the disturbance. To turn/fa) into ip(x, t), that is, appears for the first time. This linear, homogeneous, second-
to turn it into the description of a wave moving in the positive order, partial differential equation is usually taken as the
jc-direction at a speed v, we replace x wherever it appears in defining expression for physical waves in a lossless medium. There
f(x) by (jc - vt), thereby yielding ipfx, f) = 3/[10(;t - vt)2 + are lots of different kinds of waves, and each is described by
1]. If u is arbitrarily set equal to, say, 1.0 m/s and the function its own wavefunction ip(x). Some are written in terms of
is plotted successively at t = 0, t = 1 s, t = 2 s, and t = 3 s, we pressure, or displacement, while others deal with electromagnetic
get Fig. 2.4fr, which shows the pulse sailing off to the right at fields, but remarkably all such wavefunctions are solutions of
1.0 m/s, just the way it's supposed to. Incidentally, had we the same differential wave equation. The reason it's a partial
substituted (jc + vt) for x in the profile function, the resulting differential equation is that the wave must be a function of
wave would move off to the left.
If we check the form of Eq. (2.5) by examining ip after an time. A linear differential equation is essentially one
increase in time of At and a corresponding increase of v At in consisting of two or more terms, each composed of a constant
jc, we find
f[(x + vAt)- v(t + At)] ■= f{x - vt)
and the profile is unaltered.
Similarly, if the wave was traveling in the negative x-direc- Furthermore, if a differential equation is of order N, the solution
tion, that is, to the left, Eq. (2.5) would become
ip =f(x + vt), with v > 0 (2.6) equation guided by the foreknowledge (p. 14) that the most
We may conclude therefore that, regardless of the shape of the constants (amplitude and frequency or wavelength) to specify it,
disturbance, the variables x and t must appear in the function and this suggests second derivatives. Because there are two
as a unit, that is, as a single variable in the form (x + vt). independent variables (here, x and t) we can take the derivative
Equation (2.5) is often expressed equivalently as some of ip(x, t) with respect to either x or t. This is done by just
function of (t - x/v), since
/ x — vt \
f{x - vt) = Fl —I = Fit - x/v) (2.7) but to make the distinction evident the partial derivative is
The pulse shown in Fig. 2.2 and the disturbance described the partial derivative of ip(x, t) = fix') with respect to x,
by Eq. (2.5) are spoken of as one-dimensional because the holding t constant. Using x' = x + vt, and inasmuch as
waves sweep over points lying on a line—it takes only one
space variable to specify them. Don't be confused by the fact
that in this particular case the rope happens to rise up into a
second dimension. In contrast, a two-dimensional wave
propagates out across a surface, like the ripples on a pond, and can
be described by two space variables.
2.1.1 The Differential Wave Equation
In 1747 Jean Le Rond d'Alembert introduced partial Holding x constant, the partial derivative with respect to time is
differential equations into the mathematical treatment of physics. That
same year, he wrote an article on the motion of vibrating
strings in which the so-called differential wave equation
several independent variables, namely, those of space and
multiplying a function ip(x) or its derivatives. The relevant point is
that each such term must appear only to the first power; nor
can there be any cross products of ip with its derivatives, or of
its derivatives. Recall that the order of a differential equation
equals the order of the highest derivative in that equation.
will contain N arbitrary constants.
We now derive the one-dimensional form of the wave
basic of waves traveling at a fixed speed requires two
differentiating with respect to one variable and treating the other
as if it were constant. The usual rules for differentiation apply,
written as d/dx.
To relate the space and time dependencies of ip(x, t), take
#= ^
dx dx
dlb df dx' df
— =-^7 = -^7 (2-8)
dx dx dx dx
dx' d(x +Vt)
because = = 1
dx dx
dip df dx' df df
— =-^7 = -hi+v) =+17-^- (2.9)
dt dx' dt dx' dx'