一阶谓词：解析猴子取香蕉的逻辑推理

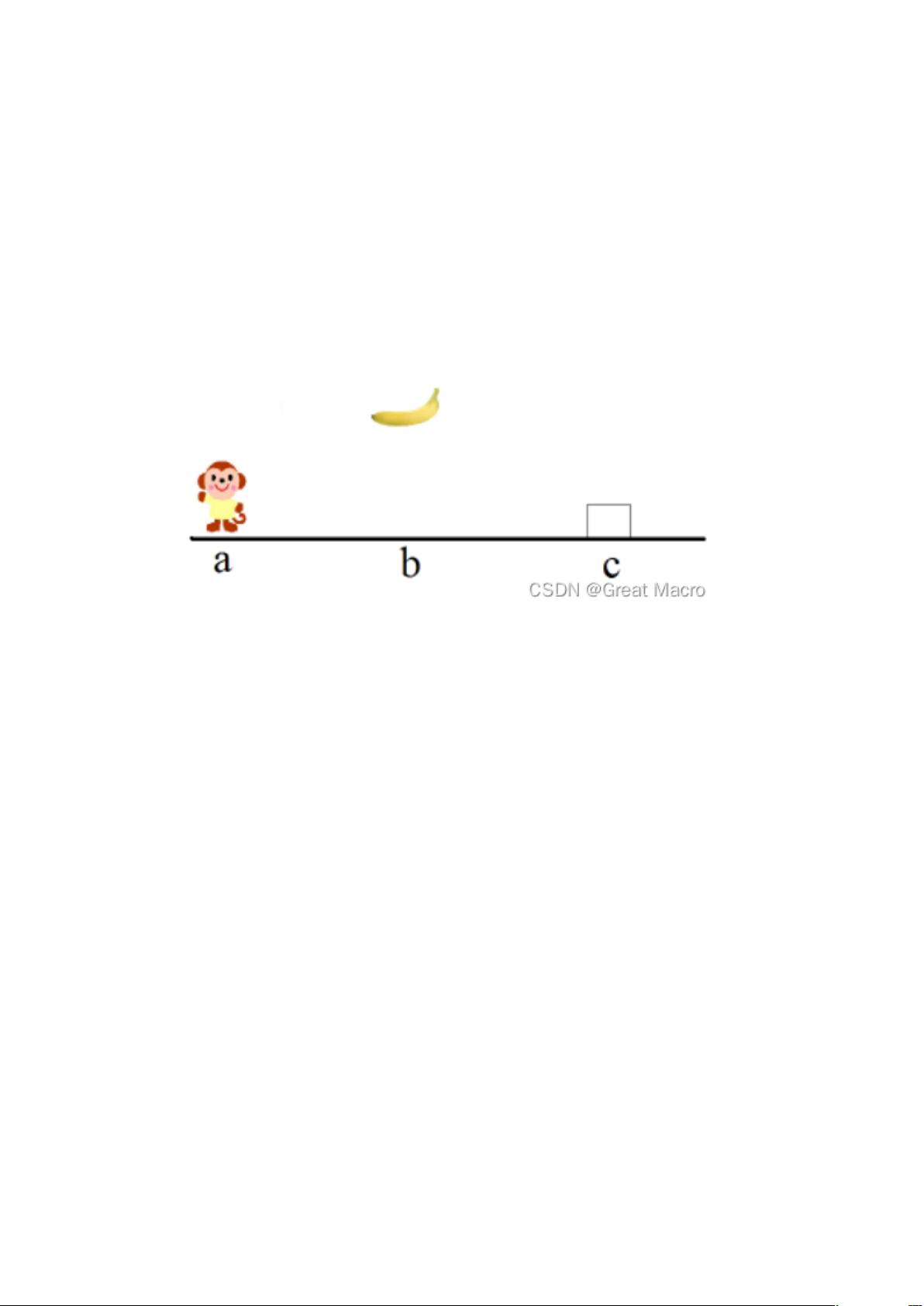
本文档标题为"123683329-3-陈宗岩.docx"，但未提供具体内容，仅有一段关于一阶谓词理论的简要介绍。一阶谓词逻辑是形式逻辑的一种，它用于描述和分析数学和计算机科学中的命题和推理。在这个上下文中，一阶谓词是指那些涉及到一个或多个个体（通常用变量表示）和它们之间的关系的陈述。文档提到的例子是猴子吃香蕉的情境，通过一阶谓词的形式来分析猴子的行为，如run、jump、push和climb，并基于这些动作来构建逻辑表达式。 在给出的代码片段中，作者使用了结构体`State`来表示猴子、箱子和香蕉的位置，以及一个数组`actionsave`来存储每个状态转换的动作。函数`monkeygoto`模拟猴子根据目标位置移动，而`movebox`则表示猴子推动箱子以改变其位置。通过这些函数，可以逐步地推理出猴子如何通过一系列动作实现获取香蕉的目标。 具体步骤如下： 1. `run(monkey,b)`：猴子跑向香蕉所在位置B。 2. `jump(monkey,b)`：如果猴子在B处不能直接取到香蕉，可能需要跳到箱子上。 3. `run(monkey,c)`：如果猴子不在箱子旁边，需要先跑到箱子C处。 4. `push(box,b)`：猴子推箱子到香蕉位置。 5. `climb(monkey,box)`：猴子爬上箱子并从箱子上跳到香蕉处。 通过这种方式，一阶谓词逻辑被用来构建和追踪状态转移的逻辑流程，从而解决实际问题。这个文档可能是在探讨如何将一阶逻辑应用于编程或者游戏设计中的状态机管理，以实现自动化的路径规划和决策制定。由于缺少完整的文档内容，无法进一步深入分析，但提供的部分展示了逻辑模型和程序设计如何结合一阶谓词来描述复杂情境。