电容式MEMS惯性传感器的机电Σ-Δ调制器力反馈接口详解

需积分: 9 110 浏览量更新于2024-07-14 收藏 5.39MB PDF 举报

本文档深入探讨了电容式微机械系统(MEMS)惯性传感器中广泛应用的机电式Sigma-Delta调制器(EM-Sigma Delta M)的力反馈接口。Sigma-Delta调制器作为一种常见的模拟信号到数字信号转换器，因其高分辨率而受到青睐。通过适当的修改，它们可以作为EM-Sigma Delta M接口，结合力反馈与模拟至数字转换的功能，同时保持相对较低的电路成本。文章首先概述了EM-Sigma Delta M接口的基本原理和设计方法，强调了它们如何优化电容式MEMS惯性传感器的数据采集性能。接下来，作者对EM-Sigma Delta M加速度计和陀螺仪进行了分类，并详细剖析了不同架构的设计特点，包括它们在噪声抑制、线性和动态范围方面的优势与挑战。讨论的重点在于代表性EM-Sigma Delta M惯性传感器系统的比较，这些系统可能采用了不同的技术，如电压模式、电流模式或混合模式，以适应不同的应用需求。它们在实际应用中的性能指标，如灵敏度、稳定性和功耗，以及针对工业环境的耐久性和鲁棒性，都被详细地评估和分析。此外，文中还涵盖了EM-Sigma Delta M接口与传统模拟接口、直接数字转化器(DAC)接口之间的比较，探讨了EM-Sigma Delta M的独特优点，如在低频信号处理中的优势以及在高动态范围测量中的性能提升。这篇综述为电容式MEMS惯性传感器的EM-Sigma Delta M力反馈接口的研究者、工程师和应用开发者提供了一个全面的参考框架，帮助他们理解和选择最适合其应用的解决方案。通过深入了解这种技术，业界能够更好地利用它来提高传感器的精度和稳定性，推动微电子技术在惯性测量领域的进步。

CHEN et al.:EM-(M) FORCE FEEDBACK INTERFACES FOR CAPACITIVE MEMS INERTIAL SENSORS: A REVIEW 6479

Fig. 4. Converting a purely electrical  M to an unconstrained

EM-M. (a) An unconstrained electrical M structure [25]. (b) The

feedback path to the inner node of the ﬁrst resonator stage can be converted

to a feedforward path. (c) The feedforward path can be shifted and replaced

by the micromechanical sensor. From [27].

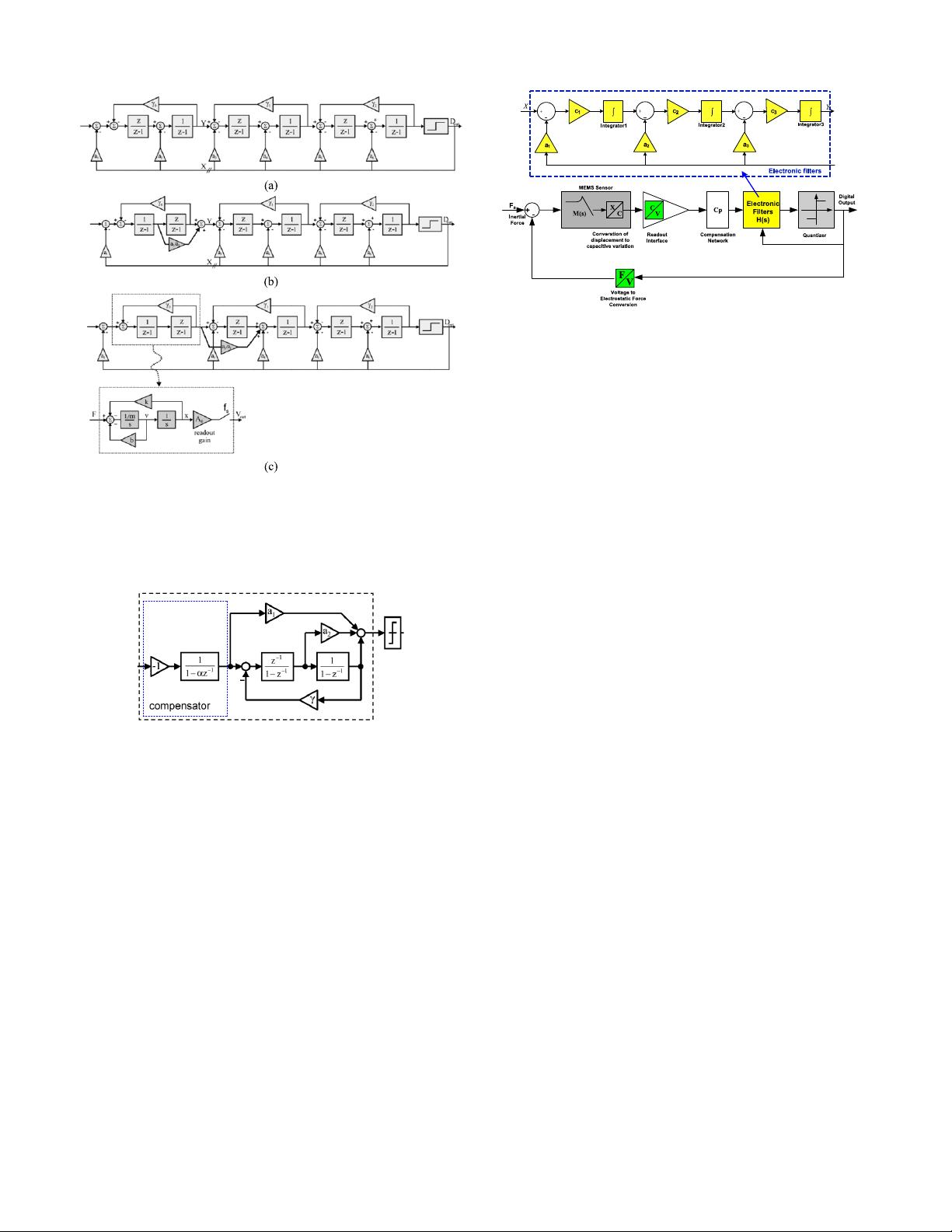
Fig. 5. Positive feedback compensator in a EM- M interface described

in [28] and [29].

Thus, the ﬁrst two electrical integrators can be replaced with

two mechanical integrators. The resulting structure retains the

same order as the original purely electrical  M, and does

not need a compensator for loop stability.

However, the unconstrained  M architecture and conven-

tional lead compensation results in stability margins that are

inadequate for high-Q (vacuum packaged) sensing elements.

This problem is due to high-order resonance modes of the

sensing element arising from the electrostatic comb ﬁngers,

which normally are sufﬁciently damped at atmospheric pres-

sure, but become highly underdamped in vacuum resulting in

a phase lag approaching −360°. Ezekwe and Boser [28], [29]

used a different compensator that utilizes positive feedback

to introduce a phase lead of 180° at all frequencies, which

is sufﬁcient to compensate the phase lag introduced by the

parasitic modes. The block diagram of the EM- M feedback

loop with positive feedback compensator is shown in Fig. 5.

Furthermore, other factors including the time delay between

the position sense and feedback pulse, the sampling

frequency f

and whether sensing and feedback use separate

Fig. 6. Cascaded integrators with distributed feedback architecture for a

EM-M [25].

or common electrodes inﬂuence the stability and performance

of the EM- M loop. This necessitates a tradeoff between

these design choices.

C. Single Loop Architectures

Several loop structures have been described for implement-

ing a single-loop high-order EM- M; they are trade-offs

between structure complexity and the freedom of choosing the

shape of the signal-transfer-function (STF) and the position of

the noise-transfer-function (NTF) zeros [30]. The most com-

monly used structure is the cascaded integrator with distributed

feedback (CIDF) architecture, as depicted in Fig. 6. It contains

a cascade of several delaying integrators with feedback signals

that are scaled by coefﬁcients a

(i = 1, 2 ...)andfedto

each integrator. The distributed feedback architecture bypasses

the mechanical sensing element and therefore contributes

compensating zeros, whose values depend on the feedback

coefﬁcients as well as the parameters of the sensing element.

Furthermore, the feedback voltage of this topology cannot be

adjusted without tuning the values of the coefﬁcients a

[30].

Dong [25] analysed the total in-band noise of a typical CIDF

architecture, which is mainly determined by the quantization

noise at the upper end of the signal band. It thus limits the

maximum obtainable signal bandwidth and it is desirable to

further reduce the total in-band quantization noise power.

A single loop high-order EM- M can be constructed by

using several local feedback paths in the loop ﬁlter to shape

the quantization noise at the end of the signal band [31].

Fig. 7 (a) and (b) show the architecture of an electronic ﬁlter

with feed-forward with local resonators (FFLR) [32], [33], and

distributed feedback loops with local resonators (DFLR) [34],

respectively. The local feedback path g

(i = 1, 2 ...) will

create a local resonator, which produces notches to cause fast

decay of the signal magnitude in the stop-band and thus further

suppresses the quantization noise. The architecture in Fig. 7(a)

does not contain signal paths bypassing the sensing element

since it is in series with the ﬁlter and the quantizer. The

feedback range is easily adjusted by varying the magnitude

of the feedback pulses.

Normally, a single loop architecture has a low susceptibility

to analog component mismatch [35]. In addition, the quanti-

zation noise is randomized by the high-order loop; therefore,

limit cycle tones are less likely to occur [25].

剩余19页未读，继续阅读

weixin_38736018

粉丝: 8
资源: 855

电容式MEMS惯性传感器的机电Σ-Δ调制器力反馈接口详解

集成电路行业：MEMS惯性传感器专题报告-大浪淘沙始见金，关注MEMS惯性传感器产业链优质标的.pdf

双量化机电Sigma-Delta调制器MEMS振动轮陀螺仪的设计

电子-一种电容式MEMS压力传感器

数字 MEMS 麦克风内部集成了四阶Sigma-Delta调制器，还需要自己设计吗

目前最先进的车载惯性传感器有哪些

mems电容传感器小电容的测量

MEMS磁敏传感器的实际应用

基于mems的电容式传感器信号调理电路设计

MEMS磁敏传感器在机器人领域的应用应用

基于嵌入式开发的传感器型号有哪些

最新资源