"数学表达式计算C语言实现——设计思想及具体实现方法"

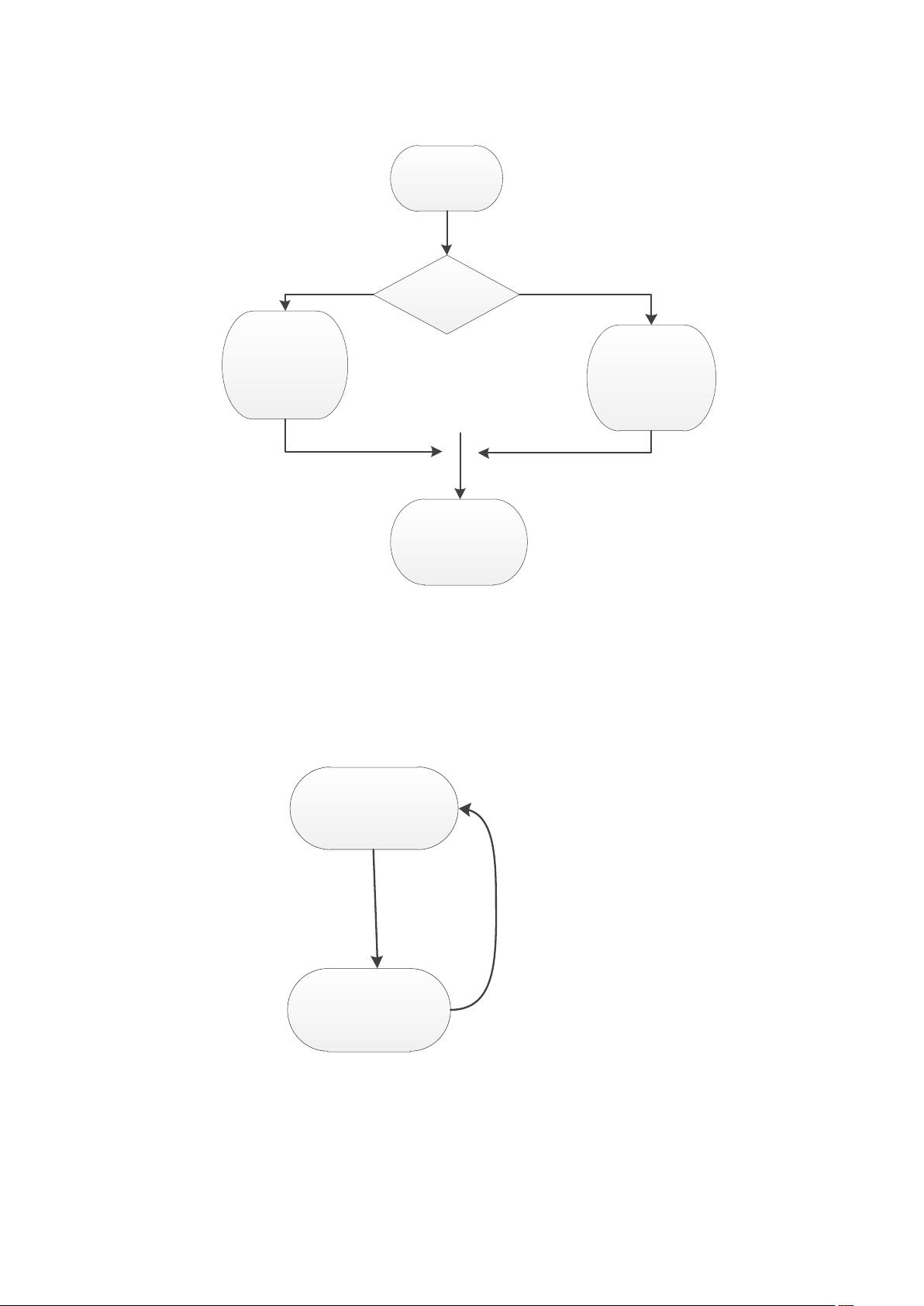
空格，用来区分不同的数字。如果是操作符，则需要判断当前操作符与操作符栈栈顶操作符的优先级，如果当前操作符优先级大于栈顶操作符，则直接将当前操作符压入操作符栈；如果当前操作符优先级小于等于栈顶操作符，则将栈顶操作符弹出，并将其存入 exp 数组中，然后将当前操作符压入操作符栈。如果当前操作符是左括号，则直接将其压入操作符栈。如果当前操作符是右括号，则需要将操作符栈中相应左括号之前的操作符依次弹出，并存入 exp 数组中，直到遇到左括号为止。处理完整个字符串后，将操作符栈中剩余的操作符依次弹出，并存入 exp 数组中，得到后缀表达式。 （2）后缀表达式计算 定义一个操作数栈 num，用来存放操作数。对 exp 数组逐个扫描，如果是数字或小数点，则将其转换为相应的数值，并压入操作数栈。如果是操作符，则从操作数栈中依次弹出两个操作数，进行相应的运算，并将结果压入操作数栈中。处理完整个数组后，操作数栈中的唯一元素即为计算结果。 二、主要函数 实现算术表达式计算的主要函数如下： 1）int priority(char c) //判断操作符优先级的函数 输入参数为一个字符，返回值为该字符对应的优先级。根据题目给出的优先级规则，可以给出相应的实现。 2）void infix_to_postfix(char* str, char* exp) //中缀转后缀函数 输入参数为一个字符数组 str 和一个字符数组 exp，分别存放中缀表达式和后缀表达式。 函数将中缀表达式转换为后缀表达式，并存放在 exp 数组中。 3）double calculate_postfix(char* exp) //后缀表达式计算函数 输入参数为一个字符数组 exp，存放后缀表达式。 函数根据后缀表达式进行计算，并返回计算结果。 三、设计细节 1）中缀转后缀函数的实现思路：使用一个操作符栈 op 和一个字符数组 exp，分别用来存放操作符和后缀表达式。对中缀表达式逐个字符进行扫描，根据字符的类型进行相应的操作。如果是数字或小数点，则直接存入 exp 数组中；如果是操作符，则需要判断其与操作符栈栈顶操作符的优先级，并进行相应的操作。扫描完整个中缀表达式后，将操作符栈中剩余的操作符依次弹出，并存入 exp 数组中，得到后缀表达式。 2）后缀表达式计算函数的实现思路：使用一个操作数栈 num，用来存放操作数。对后缀表达式逐个字符进行扫描，根据字符的类型进行相应的操作。如果是数字或小数点，则将其转换为相应的数值，并压入操作数栈；如果是操作符，则从操作数栈中依次弹出两个操作数，进行相应的运算，并将结果压入操作数栈中。处理完整个后缀表达式后，操作数栈中的唯一元素即为计算结果。 四、实例和结果 以输入表达式"2 + 3 * 4 - 5"为例，来演示整个计算过程： 1）中缀转后缀 输入表达式为"2 + 3 * 4 - 5"，将其转换为后缀表达式"2 3 4 * + 5 -"。 2）后缀表达式计算 对后缀表达式"2 3 4 * + 5 -"进行计算，得到结果为9。 五、实现代码 代码实现可以参考附件中的c文件。 总结：本文介绍了利用中缀转后缀算法实现数学表达式的计算。通过将中缀表达式转换为后缀表达式，并对后缀表达式进行计算，可以得到表达式的计算结果。实现过程中涉及到优先级判断、操作符栈和操作数栈的使用等细节。通过一个实例演示了整个计算过程，并给出了相应的代码实现。该算法可以实现多种数学表达式的计算，具有较好的灵活性和实用性。但需要注意的是，该算法仅适用于带有括号的表达式，对于不带括号的表达式可能需要进行一定的改进。