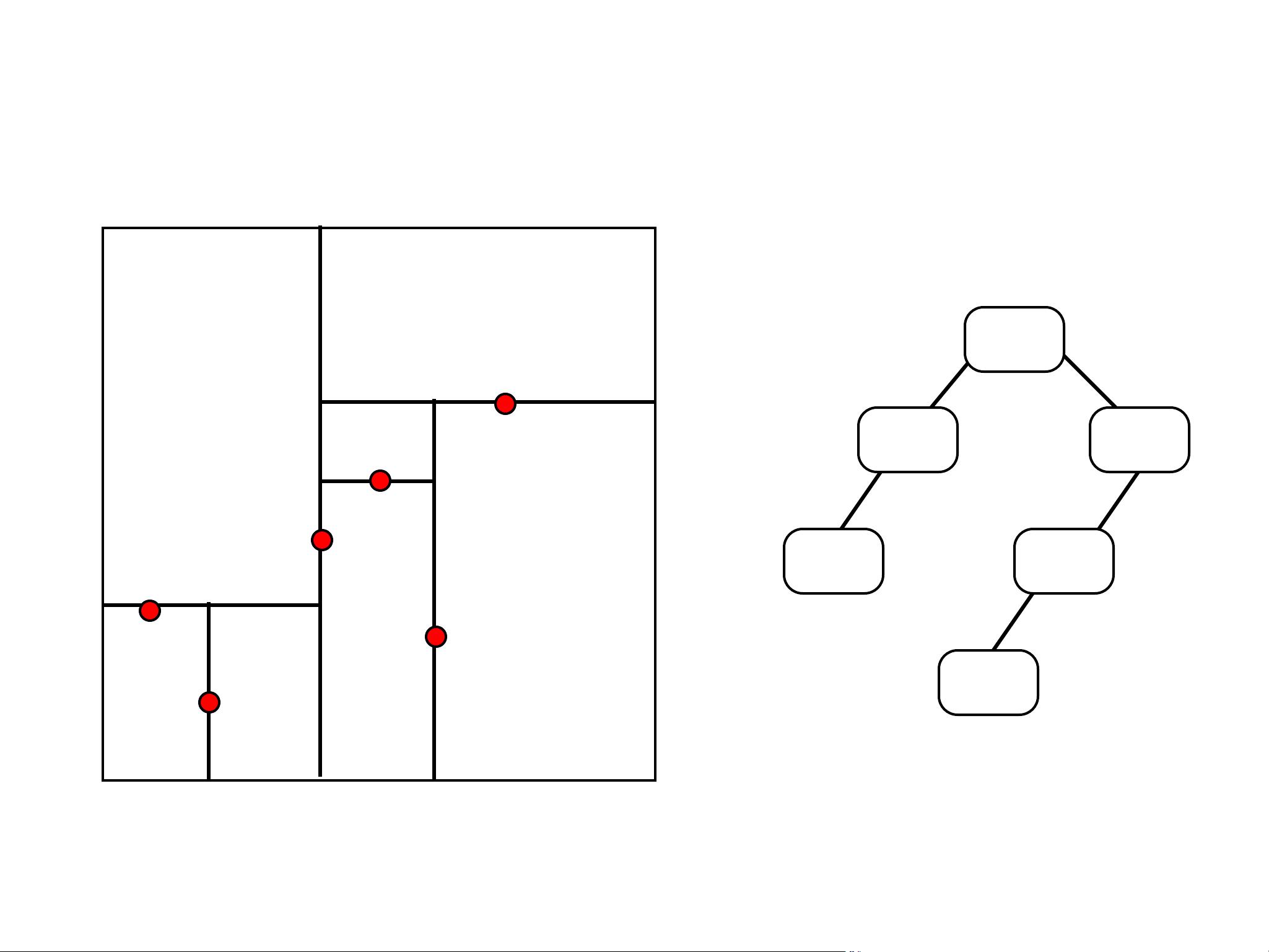
两维KD树详解:构造、插入与查找操作
需积分: 5 57 浏览量
更新于2024-07-15
收藏 143KB PDF 举报
"本文档详细解析了kd-Trees,这是一种在机器学习中常用的数据结构,特别是在最近邻分类算法中扮演着关键角色。kd-Trees最初由Jon Bentley在20世纪70年代提出,其名称来源于它能够处理任意维度的数据,例如3D、4D等,现在通常称为d维kd树。kd-Trees的核心思想是将数据空间划分为各个维度,并在每个节点进行比较,每个层次仅依赖于一个维度进行切割。
每个节点包含一个点P=(x,y),其中x和y代表坐标。查找新点(x',y')时,仅根据当前切分维度进行比较。比如如果切分维度是x,会询问x'是否小于当前节点的x值。这种设计使得查找操作非常高效,适用于对大量高维数据进行快速搜索。
插入操作是构建kd-Trees的关键部分。函数`insert(Point x, KDNode t, int cd)`负责将新点x插入到树中,参数cd表示切分维度。当遇到空节点时,创建一个新的KDNode;如果新点与当前节点数据相同,则视为错误(不允许重复);根据切分维度的大小关系决定是插入左子树还是右子树,同时递归地更新切分维度。
`findMin`函数用于查找树中第d维最小的点,通过递归遍历整个树进行查找。这个功能在搜索最近邻或执行某些排序任务时非常有用。
kd-Trees通过有效的空间划分和基于切分维度的搜索策略,实现了高维空间中的高效数据组织和查询。它们对于需要频繁的近似查询或者范围搜索的应用场景(如数据库索引、计算机视觉中的特征匹配等)具有重要意义。理解并掌握kd-Trees的工作原理和操作方法,对于任何从事机器学习特别是数据结构优化的开发者来说都是至关重要的技能。"
2019-08-16 上传
2021-07-07 上传
2024-12-01 上传
2024-12-01 上传
2024-12-01 上传
2024-12-01 上传
2024-12-01 上传
2024-12-01 上传
2024-12-01 上传
ProfSnail
- 粉丝: 4169
- 资源: 3
最新资源
- Angular实现MarcHayek简历展示应用教程
- Crossbow Spot最新更新 - 获取Chrome扩展新闻
- 量子管道网络优化与Python实现
- Debian系统中APT缓存维护工具的使用方法与实践
- Python模块AccessControl的Windows64位安装文件介绍
- 掌握最新*** Fisher资讯,使用Google Chrome扩展
- Ember应用程序开发流程与环境配置指南
- EZPCOpenSDK_v5.1.2_build***版本更新详情
- Postcode-Finder:利用JavaScript和Google Geocode API实现
- AWS商业交易监控器:航线行为分析与营销策略制定
- AccessControl-4.0b6压缩包详细使用教程
- Python编程实践与技巧汇总
- 使用Sikuli和Python打造颜色求解器项目
- .Net基础视频教程:掌握GDI绘图技术
- 深入理解数据结构与JavaScript实践项目
- 双子座在线裁判系统:提高编程竞赛效率