快速ε-最优离散追踪学习自动机：大型行动领域的新方法

136 浏览量更新于2024-08-27 收藏 1.12MB PDF 举报

"这篇研究论文是关于快速且Epsilon最优的离散追踪学习自动机，发表在2015年10月的IEEE Transactions on Cybernetics期刊上，由Jun Qi Zhang, Cheng Wang和Meng Chu Zhou (IEEE Fellow)共同撰写。" 在强化学习领域，学习自动机（Learning Automata, LA）是一种强大的工具。离散追踪学习自动机（Discretized Pursuit Learning Automata, DPLA）是其中最为流行的一种。DPLA在每个迭代周期内包含三个基本阶段：1) 选择下一个动作；2) 找到最优估计动作；3) 更新状态概率。然而，当动作的数量非常大时，学习过程会变得极其缓慢，因为每个迭代中需要进行太多更新，主要来自第一阶段的动作选择和第三阶段的状态概率更新。针对这个问题，论文提出了一种新的快速离散追踪学习自动机，保证了ε-最优性。这种方法的关键在于，它将第一阶段的动作选择和第三阶段的状态概率更新的计算复杂度独立于动作的数量，从而大大减少了计算量。这使得新方法在处理大量动作的情况下，仍能保持高效运行。此外，尽管具有较低的计算复杂度，这种新型学习自动机在静态环境中的收敛速度比传统方法更快。这一改进对于那些需要高效强化学习的大型规模、动作导向的应用场景来说，具有显著的促进作用。论文的贡献在于提供了一种优化策略，使得DPLA能够在保持性能的同时，适应更复杂的决策问题，扩展了LA在大规模行动领域的应用潜力。

ZHANG et al.: FAST AND EPSILON-OPTIMAL DISCRETIZED PURSUIT LA 2091

Fig. 2. DP

using r = 3andn = 5, a

is the estimated optimal action and

positive response is received. DP

(a) initialization and (b) state probability

update when the chosen action is rewarded.

the state probability of the action with the highest estimate

has to be increased by an integral multiple of the smallest

step size . When the chosen action is penalized, there is

no updating in the state probability vector, and it is thus of

the reward-inaction paradigm. Assume that m is the index of

the estimated optimal action. The update scheme of DP

described brieﬂy as follows [1], [36].

Phase 1: Select the next action.

Select an action a(t) = a

according to the probability distri-

bution P(t). Update H

, G

and



Phase 2: Find the optimal estimated action

m = argmax

{



Phase 3: Update the state probability.

If β(t) = 1 Then

(t + 1) = max

j=m

(t) − , 0}, ∀j ∈ N

(2)

(t + 1) = 1 − 

j=m

(t + 1). (3)

Else

(t + 1) = p

(t), ∀j ∈ N

. (4)

Endif

III. F

AST DISCRETIZED PURSUIT LA

In this section, FDP

is proposed by exploiting the most

signiﬁcant pattern of the discretized update scheme in DP

This pattern always increases the state probability of the esti-

mated optimal action but decreases others by discretized step

 = 1/(rn) where r is the number of allowable actions, and

n is a resolution parameter.

Once an update occurs, (r − 1) ∗  are rewarded to the

estimated optimal action and other actions are all penalized

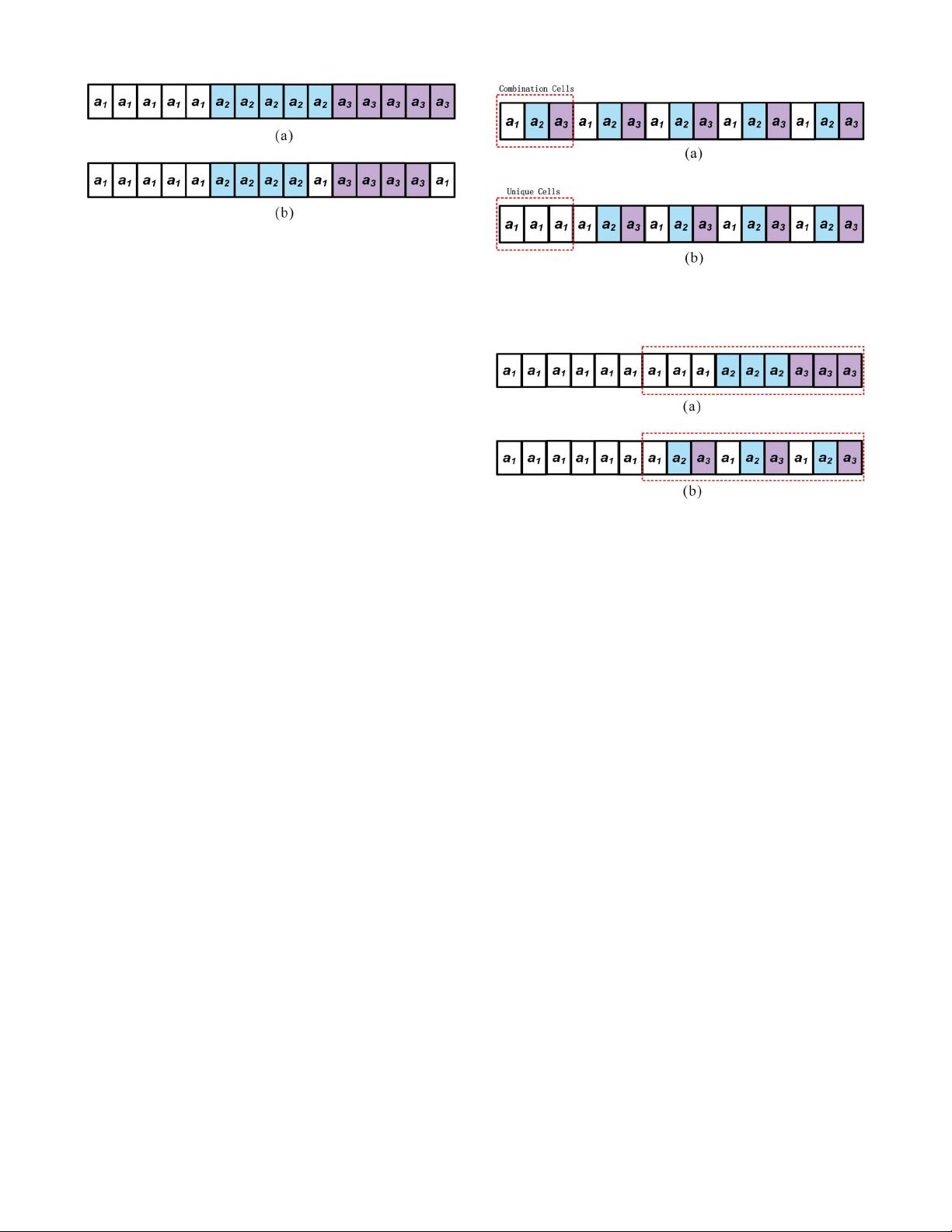
by .Fig.2 illustrates this update scheme. Each  is consid-

ered as a probability cell (PC) shown in Fig. 2(a). Assume a

the estimated optimal action and positive response is received,

(r − 1) PCs are rewarded to a

and one PC is penalized for

other actions as shown in Fig. 2(b), respectively.

A. Fast Probability Update

In the proposed FDP

, r PCs from each action are initially

composed as a combination (C) unit in Fig. 3(a). n C units

are initialized and equivalent to the one for DP

in Fig. 2(a).

When an update occurs, a C unit is transformed to a unique (U)

unit which is composed r PCs of a

as shown in Fig. 3(b).

This updating result is equivalent to the one for DP

as shown

in Fig. 2(b).

Fig. 3. FDP

using r = 3andn = 5, a

is the estimated optimal action

and it received positive response. FDP

(a) initialization and (b) rewarded

when C ≥ 1.

Fig. 4. U-C transformation: r = 3andn = 5. (a) All U units. (b) U-C

transformation.

Thus, the computational complexity to update the prob-

ability is reduced from O(r) to O(1) in FDP

because a

type transformation from a C unit to a U unit can ﬁnish the

probability updating.

B. U-C Transformation

In FDP

, n C units are initialized. When the probability

update continues, the C units can be used up and transformed

into the U units. Fig. 4 shows that r U units can be trans-

formed into r C units and they are equivalent. In this way, the

transformed C units can be available for the subsequent fast

probability update.

C. Reorganization

An action a

is active if its state probability p

(t) is nonzero.

When the state probability of an active action turns to be

zero as shown in Fig. 5(a), reorganization is triggered as

shown in Fig. 5(b). Reorganization lets ˜r =˜r − 1 and set

this action as nonactive state where ˜r is number of the active

actions and initially ˜r = r. Hence, the step size turns to be

 = 1/(˜rn). The step size of the update scheme in FDP

for p

(t) “increases” because more and more state probabili-

ties turn to be zero such that the number of the active actions

decreases with the learning process. It means that the step size

is “accelerated” along with the learning process. It is reason-

able because the number of times for which active actions

are selected increases and the reward probability estimation

of active actions becomes more and more accurate along with

the learning process.

Then the U-C transformation is called to transform U units

into C units for the subsequent fast probability updating. As

剩余10页未读，继续阅读

weixin_38662367

粉丝: 5
资源: 912

快速ε-最优离散追踪学习自动机：大型行动领域的新方法

下推自动机详解：FL&A第七讲的构造与工作原理

清华大学《形式语言与自动机》考试试题

用OpenFst工具实现非循环概率有限状态自动机间预期编辑距离算法

使用Q学习和epsilon贪婪策略解决方形迷宫：使用涉及epsilon贪心策略的Q学习算法解决随机生成的正方形迷宫。-matlab开发

TD learning,PER和Epsilon：深度学习对高等教育教学的启示.pdf

正则表达式和有穷自动机

epsilon:通过Websockets进行简单，快速和有趣的通信

turingMachine:图灵机和自动机的实现

epsilon:Epsilon是一个以纯C语言编写的具有机器学习和统计功能的库

确定性清洁机器人的 Q-learning（无模型值迭代）算法：使用 Q-learning 和 epsilon-greedy 探索的强化学习示例-matlab开发

最新资源