"线性代数讲座: 矩阵和行列式，伴随矩阵与标准形，解题技巧与典型例题"

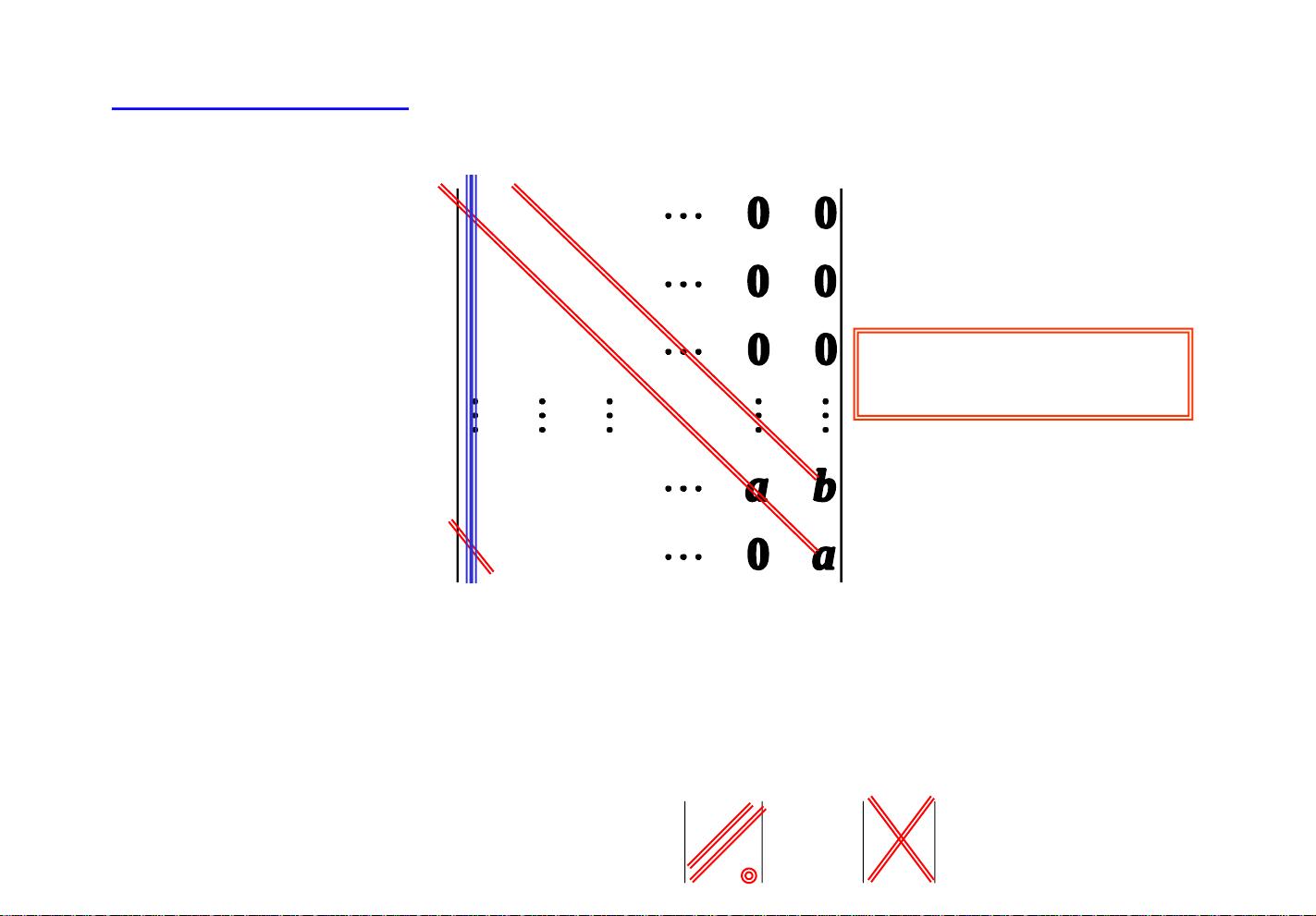
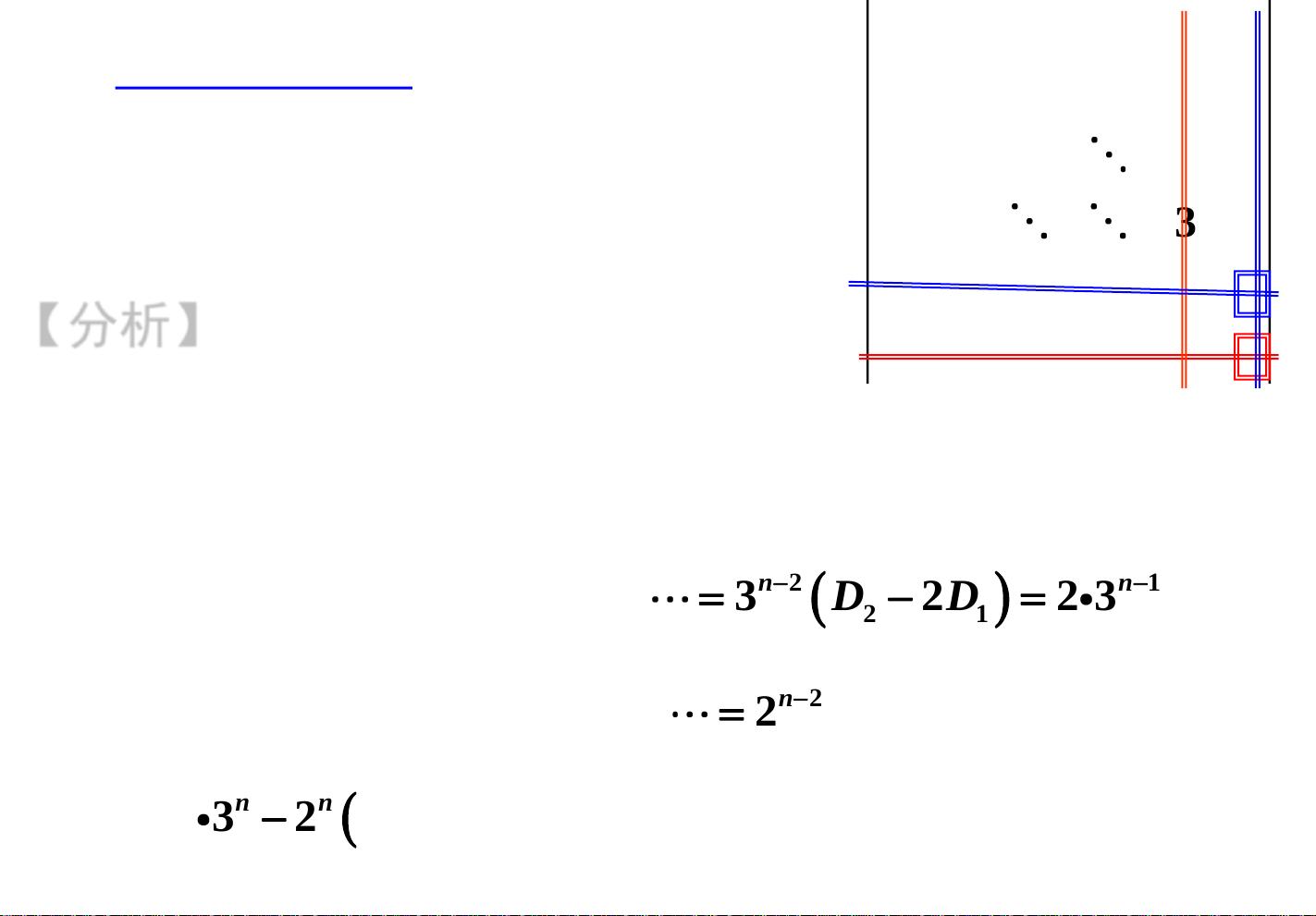
线性代数讲座的1, 2章主要涵盖了伴随矩阵A*、行列式计算、矩阵等式、初等变换与初等矩阵、矩阵的标准形、以及典型例题的讲解。在第一讲中，我们首先介绍了伴随矩阵的定义，即对于一个n阶矩阵A，其伴随矩阵A*的定义为其每个元素的代数余子式构成的矩阵，即A*=(Aij)T，其中Aij=(-1)^(i+j)Mij，Mij为A中划去第i行第j列后得到的（n-1）阶矩阵的行列式。我们还介绍了伴随矩阵与原矩阵的基本关系式和衍生关系式，以及伴随矩阵的秩的计算方法。除此之外，我们还通过例题演练了伴随矩阵在行列式计算中的应用，使学生能够灵活运用伴随矩阵的性质求解具体问题。 其次，我们讨论了行列式的计算方法，包括通过初等变换和化简得到行列式的值。我们介绍了基本的行列式计算规则，以及通过行列式的性质求解行列式的值的方法。通过例题讲解，学生能够在实际问题中熟练应用行列式的计算方法，加深对行列式的理解。同时，我们还介绍了矩阵等式的性质和解题方法，通过实例讲解，帮助学生更好地理解矩阵等式的求解过程和技巧。 在第一讲的最后部分，我们讨论了初等变换与初等矩阵的关系，以及矩阵的标准形。我们介绍了初等矩阵的定义和性质，以及初等变换和初等矩阵之间的联系，通过例题讲解帮助学生掌握初等变换和初等矩阵的应用方法。同时，我们还介绍了矩阵的标准形的定义和性质，通过实例讲解帮助学生理解矩阵的标准形对矩阵的性质和结构的描述。在典型例题的选讲部分，我们选择了一些典型的例题进行讲解，帮助学生掌握线性代数中的重点和难点，增加他们在解题时的信心和能力，提高他们的解题效率。 总之，本讲座通过伴随矩阵A*、行列式计算、矩阵等式、初等变换与初等矩阵、矩阵的标准形和典型例题讲解，帮助学生巩固了线性代数的基本知识，提高了他们的学习兴趣和学习效果，为他们的学习和应用线性代数打下了坚实的基础。通过本讲座的学习，学生能够更好地理解线性代数的概念和方法，提高其数学分析和问题解决的能力，在学业和科研中取得更好的成绩和进步。