"Python模拟蒙特卡罗法计算不规则图形面积研究"
需积分: 0 78 浏览量
更新于2023-12-06
2
收藏 5.1MB PDF 举报
实际问题中,我们也会遇到一些不规则图形,如心形、星形、曲线图形等。这些图形的面积计算不再像规则图形那样直接使用公式计算,而是需要通过数值积分或近似计算的方法进行求解。蒙特卡洛法是一种常用的近似计算方法,通过随机投点和统计的方式,可以用于计算不规则图形的面积。
在本研究中,我们主要关注蒙特卡洛法在计算不规则图形面积中的应用。我们首先通过撒豆法来验证蒙特卡洛法的可行性,然后通过Python语言编写了一个基于蒙特卡洛算法的面积计算程序,该程序可以用于任意图形的面积计算。我们使用编写的程序对蒙特卡洛法面积算法进行了模拟运算,并在归纳总结的过程中得到了两个重要的结论:随着随机点的数量增加,计算出的面积就会越来越精确;多次取平均可以增加结果的准确性。
二. 蒙特卡洛法在不规则图形面积计算中的原理和方法
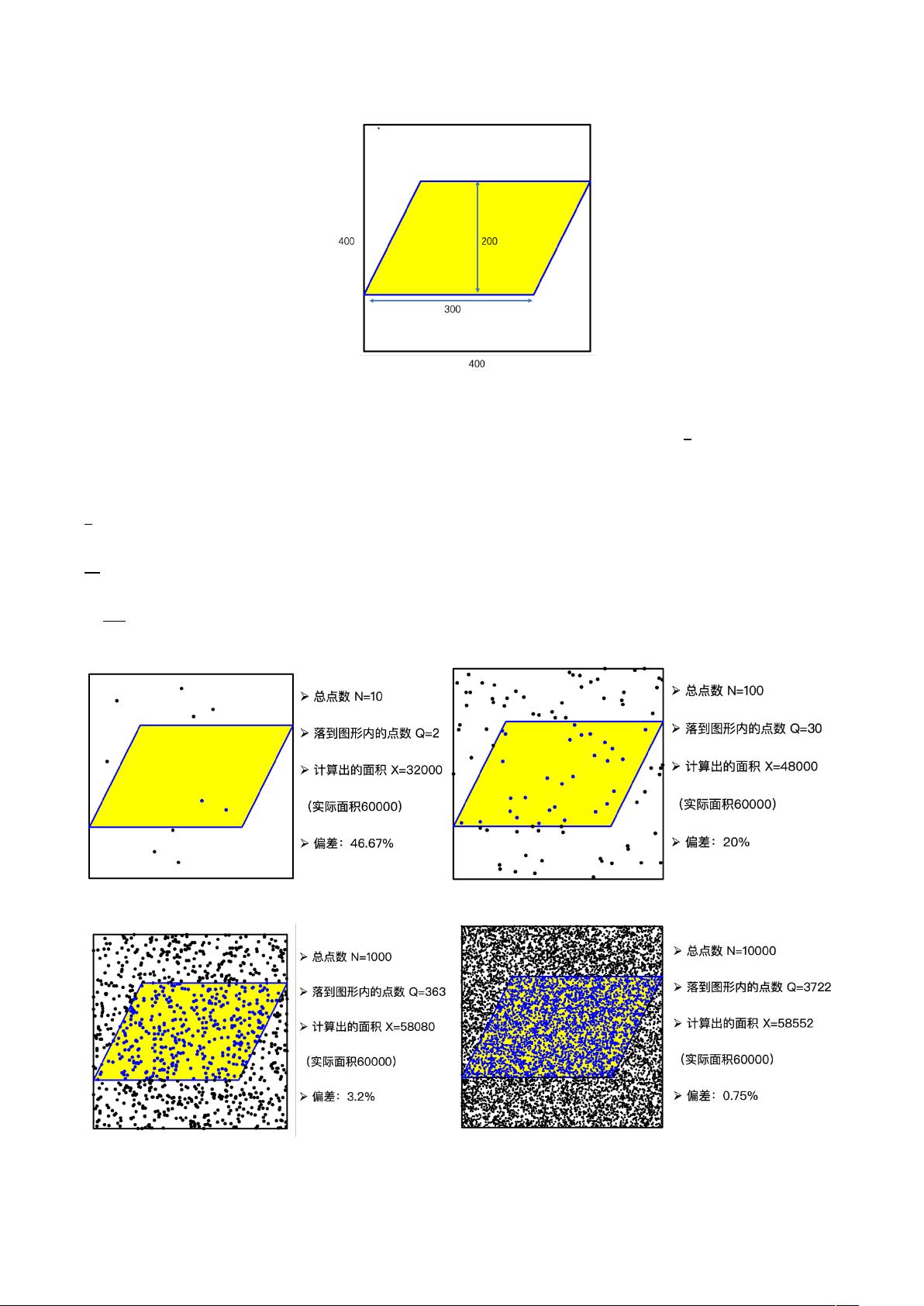
蒙特卡洛法在计算不规则图形的面积时,主要包括以下步骤:1)构造包围不规则图形的矩形边界;2)在矩形内随机生成大量的点;3)统计落在不规则图形内部的点的数量;4)通过统计点的数量和总点数的比值,乘以矩形的面积,即可得到不规则图形的近似面积。蒙特卡洛法的核心思想是通过大量的随机点来近似表示不规则图形的面积,从而实现面积的计算。
蒙特卡洛方法的优点在于其计算过程较为简单直观,而且可以应用于各种复杂的不规则图形。然而,其缺点也是显而易见的,就是需要大量的随机点来进行计算,因此计算量大,运算时间长。另外,蒙特卡洛方法的精度受随机因素的影响,需要通过增加随机点数量和多次取平均的方式来提高计算结果的准确性。
三. 基于Python的蒙特卡洛算法实现
我们使用Python语言编写了一个基于蒙特卡洛算法的面积计算程序。程序的实现主要包括以下几个步骤:1)构造一个矩形边界,确定不规则图形的包围矩形大小;2)通过随机数生成器,在矩形内随机生成大量的点;3)统计落在不规则图形内部的点的数量;4)通过统计点的数量和总点数的比值,乘以矩形的面积,即可得到不规则图形的近似面积。程序的实现是通过循环计算随机点的数量及统计的方式,最终可以得到不规则图形的近似面积。
四. 模拟运算及得出的结论
在我们的研究中,我们通过编写的程序对蒙特卡洛法面积算法进行了模拟运算,并得出了两个重要的结论。首先,随着随机点的数量增加,计算出的面积就会越来越精确。这一结论符合蒙特卡洛方法的原理,即通过增加随机点的数量可以提高计算结果的准确性。其次,多次取平均可以增加结果的准确性。我们发现,在进行多次模拟运算后,取平均可以减小随机误差,从而提高计算结果的准确性和稳定性。
五. 结论
通过对蒙特卡洛法在计算不规则图形面积中的研究和模拟实验,我们得出了结论:增加随机点的数量和多次取平均可以提高计算结果的准确性。因此,蒙特卡洛法在计算不规则图形面积时具有较高的可行性和精度。同时,我们通过Python语言编写的程序也验证了蒙特卡洛法的有效性和实用性,该程序可以用于任意图形的面积计算。这一研究结果对于不规则图形面积的计算具有一定的理论和实践意义,对于相关领域的研究和应用具有一定的参考价值。
5878 浏览量
153 浏览量
1487 浏览量
109 浏览量
120 浏览量
2024-11-12 上传
2024-11-12 上传
2024-11-03 上传
2024-02-22 上传