MATLAB实现的人脸识别系统设计

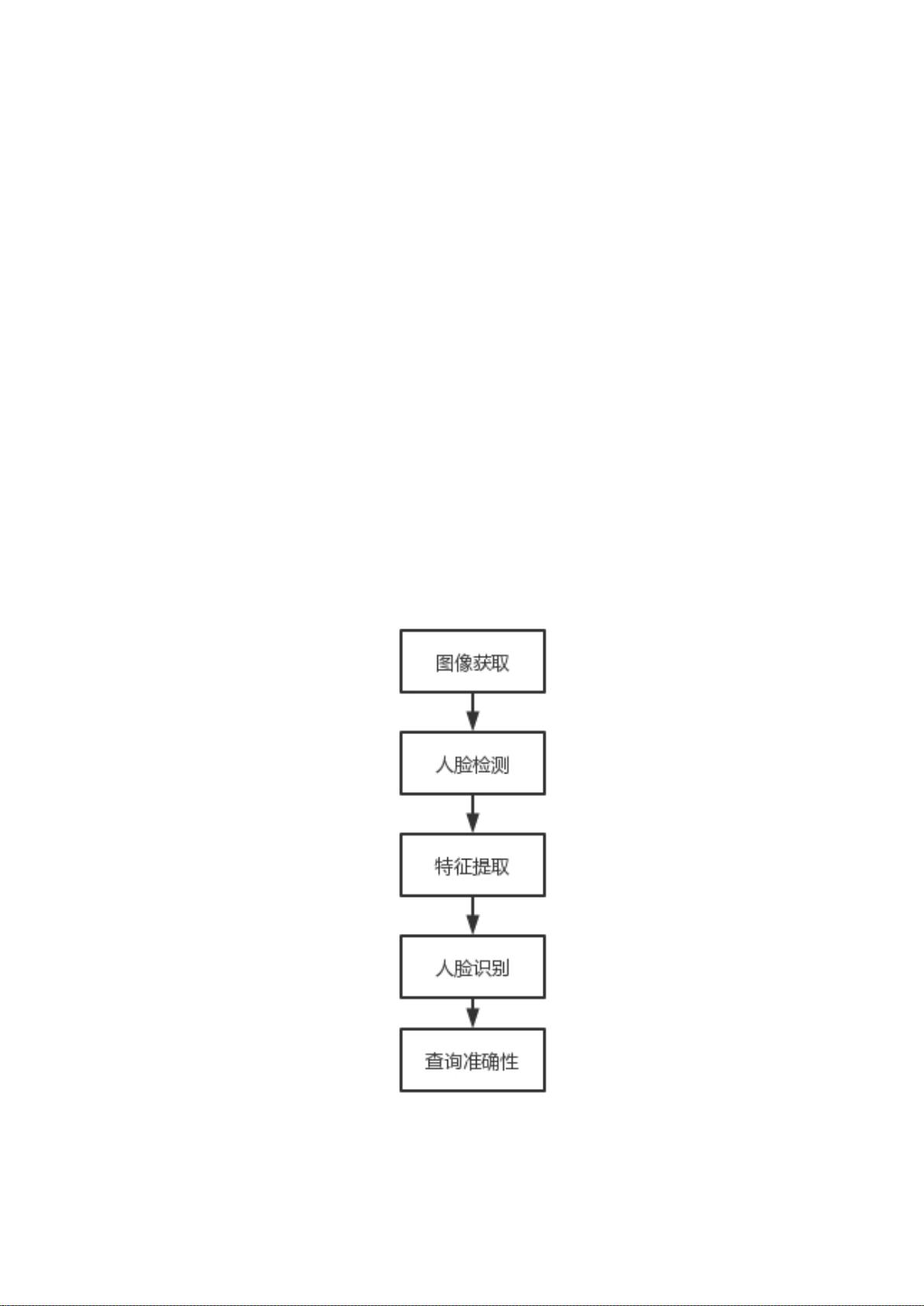
"基于MATLAB的人脸识别系统设计与实现，主要涉及PCA算法和最小距离法。" 本项目旨在设计和实现一个人脸识别系统，利用MATLAB作为开发工具。人脸识别技术是一种生物特征识别技术，它通过分析和比较人脸的视觉特征信息来识别或验证个体身份。在MATLAB环境下，该系统采用的主要算法包括主成分分析(PCA)进行特征提取，以及最小距离法进行图像识别。 1. PCA算法在人脸识别中的作用： PCA是一种统计方法，用于将高维数据转换到一个低维子空间，同时保持数据集中的方差最大化。在人脸识别中，PCA用来降低图像的维度，减少计算复杂性，并提取最具代表性的特征。首先，通过计算训练样本库中所有图像的协方差矩阵，找到其特征向量（即特征脸），这些特征向量形成的新子空间可以捕获图像的主要变化。然后，每个原始图像被投影到这个子空间中，形成低维表示。 2. 最小距离法识别： 在PCA得到的低维子空间中，新输入的人脸图像也会被投影成一个点。识别过程是通过计算新点与数据库中所有已知图像点的距离，找出最近的那个点，即与新输入图像最相似的图像，该图像对应的人脸就是识别结果。 3. 实验条件与工作基础： 该系统依赖于已知的图像数据集，以及MATLAB编程环境。图像数据集包含每张人脸图像在子空间的坐标，新输入的图像经过相同处理后，使用最小距离法进行匹配。此外，系统还需要进行人脸特征点的检测与标定，以获取关键特征，如眼睛、鼻子、嘴巴的位置和形状信息。 4. 特征提取： 特征提取是人脸识别的关键步骤，它包括对人脸特征点的检测和描述。通过检测到的眼睛、眉毛、鼻子和嘴巴等关键部位，系统可以提取全局特征（如面部整体形状）和局部特征（如眼睛大小）。PCA则进一步从这些特征中提取统计特征，通过保留协方差矩阵的主要特征值和对应的特征向量，构建K-L变换矩阵，从而得到人脸的低维表示。 5. 数据集处理： 训练样本库中的每张人脸图像被表示为一个128*128像素的矩阵，然后转置成16384*1的列向量，组成数据矩阵X。这个矩阵用于PCA算法的计算，以构建识别模型。 基于MATLAB的人脸识别系统利用PCA算法进行特征降维，通过最小距离法实现图像匹配，提供了一种高效且实用的面部识别解决方案。通过不断优化和调整，这种系统在实际应用中可以提高人脸识别的准确性和效率。