理解与应用：均值漂移算法的兴起与发展

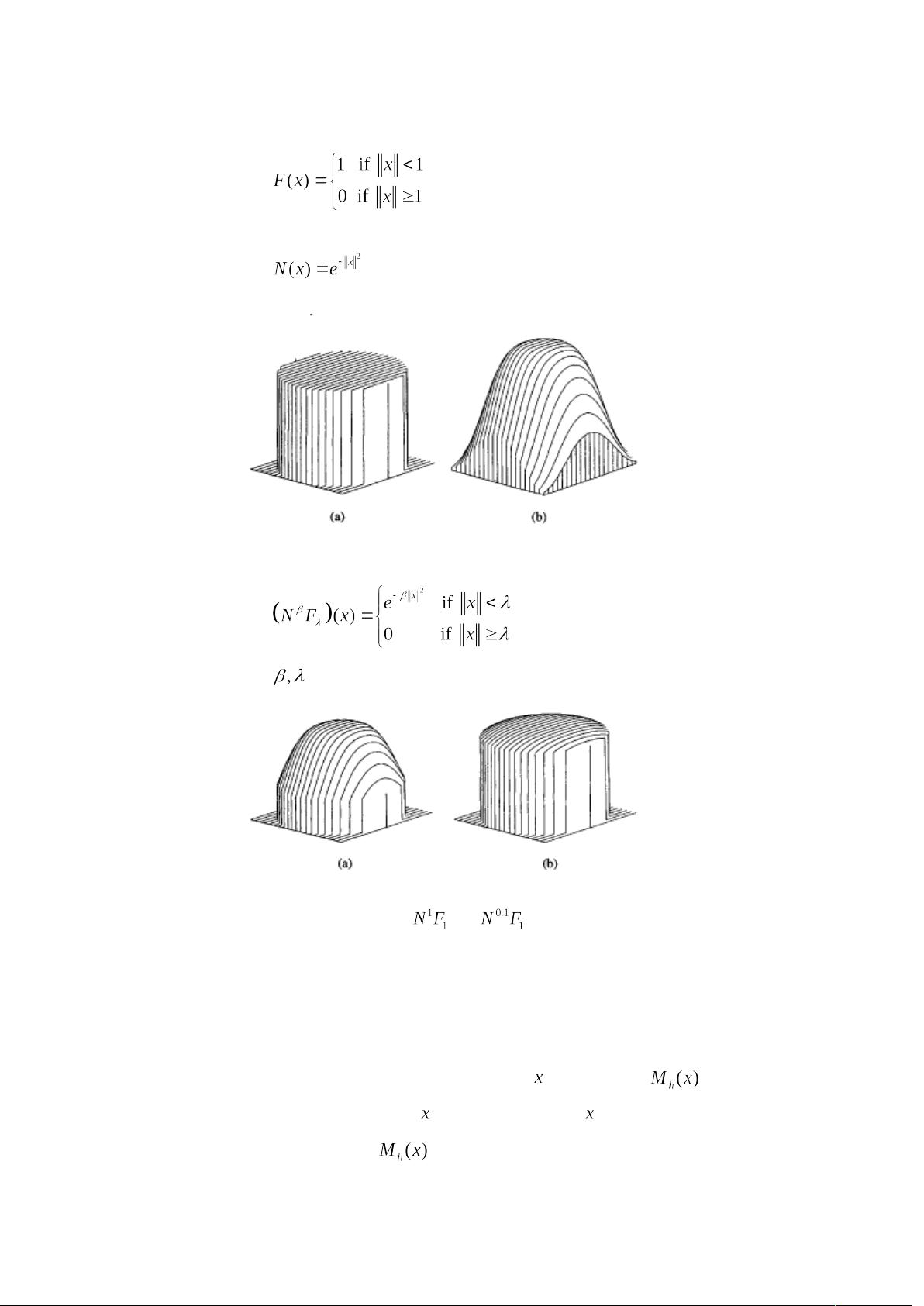
均值漂移(Mean Shift)是一种无参数的非监督学习方法，最初由Fukunaga等人在1975年的论文中引入，用于估计概率密度函数的概率密度梯度。它的核心思想是通过迭代地将每个数据点移动到其局部概率密度最大的方向，直至达到稳定状态，从而发现数据的分布模式或聚类结构。 最初的Mean Shift仅是一个向量的概念，表示数据点基于当前位置的偏移方向。然而，随着时间的推移，特别是Yizong Cheng在1995年的关键论文中，Mean Shift的意义得到了扩展。Cheng引入了核函数，使得距离对偏移量的影响可调整，这样可以根据样本点的不同距离赋予不同的权重，提高了算法的灵活性。此外，他还明确了Mean Shift在实际应用中的潜力，如图像处理中的应用，如图像平滑和分割。 Comaniciu等人进一步发展了Mean Shift，将其成功应用于特征空间分析。他们证明了在特定条件下，Mean Shift算法能收敛到概率密度函数的极大值点，这使得它成为寻找数据集中潜在模态的有效工具。同时，他们将非刚体跟踪问题转化为Mean Shift优化问题，实现了实时的物体追踪。 基本的Mean Shift算法定义在d维空间中，给定n个样本点，每个点的Mean Shift向量由以下公式给出： \[ \textbf{v}_i = \frac{\sum_{j=1}^n K_h(\textbf{x}_i - \textbf{x}_j) (\textbf{x}_j - \textbf{x}_i)}{\sum_{j=1}^n K_h(\textbf{x}_i - \textbf{x}_j)} \] 其中，\( K_h \) 是一个核函数，\( h \) 是一个带宽参数，它决定了邻域内的影响程度。随着\( h \) 的变化，Mean Shift可以捕捉到不同尺度的结构。 在后续章节中，Mean Shift的实现会详细阐述其背后的物理原理，包括如何处理多模态分布、如何选择合适的核函数和带宽、以及如何在实际应用中优化计算效率。最后，将深入探讨Mean Shift在聚类分析、图像处理（如平滑和分割）、以及实时物体跟踪中的具体应用场景，展示了其强大的适应性和广泛的应用价值。