统计回归模型详解：多项式回归分析

"该讲稿主要讲解了统计回归模型，包括回归分析的基本概念、多项式回归的细节，以及如何在实际应用中使用多项式回归进行数据建模和预测。" 回归分析是统计学中用于研究变量间关系的重要方法，旨在通过数学函数揭示变量间的依赖关系。在统计回归模型中，我们通常关注的是因变量（Y）如何受一个或多个自变量（X）的影响。回归函数可以用来描述这种关系，并基于观测数据进行统计推断，例如估计参数、检验假设等。 一元多项式回归是回归分析的一个基础类型，用于处理因变量与自变量之间非线性的关系。一元多项式回归模型的一般形式为 y = β0 + β1x + ... + βmx^m + ε，其中β0到βm是模型参数，ε表示随机误差项。当数据呈现出二次或更高次的函数关系时，可以选择多项式回归。 在实际操作中，可以使用MATLAB中的`polyfit`函数来估计多项式回归的模型参数。`polyfit(x, y, m)`返回最高次数为m的多项式系数估计值，x和y是对应的数据点。如果同时指定`[p, S] = polyfit(x, y, m)`，则S是一个矩阵，用于估计预测误差。 预估模型的输出值可以通过`polyval`函数完成，如`Y = polyval(p, X)`，其中p是`polyfit`的输出，X是新的自变量值，这将给出在X处的预测值Y。若需要误差估计，可使用`[Y, DELTA] = polyval(p, X, S)`，其中DELTA代表误差。 预测值的置信区间可以通过`polyconf`函数获取，`[Y, DELTA] = polyconf(p, X, S, alpha)`，默认显著性水平alpha为0.05，给出1-alpha置信区间的预测值Y±DELTA。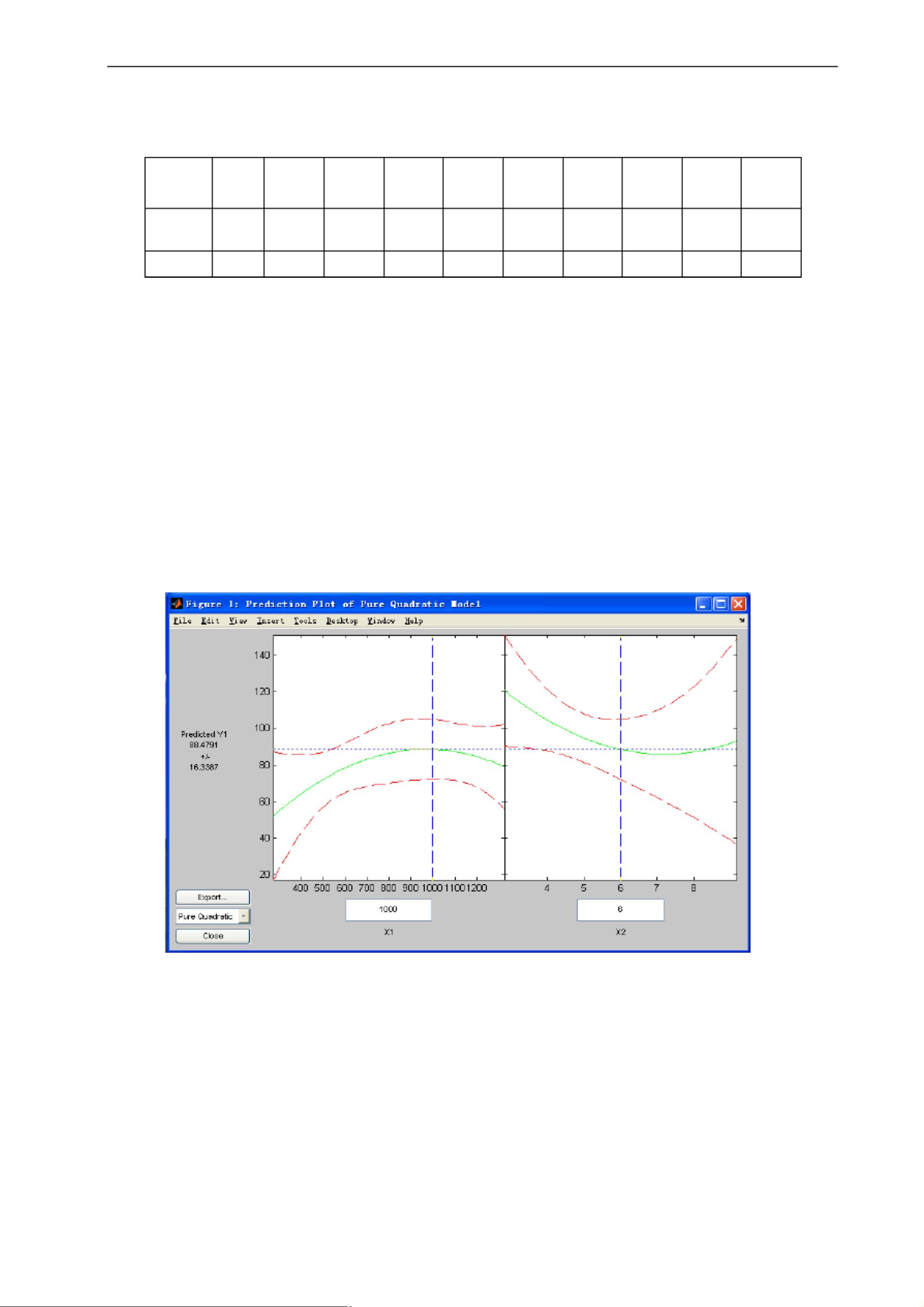 此外，MATLAB还提供了交互式工具`polytool`，方便用户可视化拟合过程和结果。例如，`polytool(x, y, m)`可绘制m次多项式拟合图，默认m为1。 举例来说，当我们观察到物体降落的距离s与时间t的关系时，可以构建一元多项式回归模型。例如，给定的数据为： | t (s) | s (cm) | |-------|--------| | 1/30 | 11.86 | | 8/30 | 61.49 | | 2/30 | ... | 通过应用上述方法，我们可以估计s关于t的多项式回归模型，从而预测不同时间下的降落距离。这个例子展示了回归分析在实际问题中的应用，即通过数据建模来预测未知情况的结果。