BD-GMD：MIMO广播信道的块对角几何均值分解
需积分: 50 134 浏览量
更新于2024-09-08
1
收藏 426KB PDF 举报
"几何均值分解（Geometric Mean Decomposition, GMD）是矩阵理论中的一个特殊分解方法，尤其在无线通信领域有重要应用。它将任意大小为m*n的矩阵X分解为QRP'的形式，其中Q和P是酉矩阵，即它们的逆等于它们的转置，而R是一个k*k维的实正上线性三角矩阵，k是矩阵X的秩。GMD的独特之处在于，R的主对角线上的元素是X的所有正奇异值的几何平均数。这种方法在处理多输入多输出（MIMO）广播信道问题时，能够帮助实现更有效的信号处理策略。
在MIMO广播信道的研究中，尤其是在使用脏纸编码（Dirty Paper Coding, DPC）来逼近信道容量方面，几何均值分解有着重要的作用。论文中提出的块对角几何均值分解（Block Diagonal Geometric Mean Decomposition, BD-GMD）是GMD的一种扩展，它将MIMO广播信道分解为多个具有相同信噪比（SNR）/信干比（SINR）的子信道，使得可以对每个用户的子信道应用等速率编码。这提高了系统性能，且易于实现。
此外，BD-GMD还进一步发展为块对角统一信道分解（Block Diagonal Uniform Channel Decomposition, BD-UCD），这个扩展允许实现MIMO广播信道的容量。通过结合DPC与BD-GMD或BD-UCD，提出的方案在模拟实验中展现出优于传统方法的性能，这对于提高MIMO系统的通信效率和质量具有重要意义。"
这篇描述涉及的知识点包括：
1. 几何均值分解（GMD）：一种矩阵分解方法，用于将矩阵分解为酉矩阵和上三角矩阵的乘积，主对角线元素是奇异值的几何平均。
2. 酉矩阵：矩阵的逆等于其转置的矩阵，通常在复共轭和正交变换中出现。
3. 上三角矩阵：矩阵下方所有非对角线元素都为零的矩阵，方便计算和表示矩阵的特性。
4. 正奇异值：矩阵奇异值中的正值，对于实对称矩阵，它们是特征值的平方根。
5. MIMO技术：利用多个天线在发射端和接收端同时传输和接收信号，以提高无线通信系统的容量和可靠性。
6. 脏纸编码（DPC）：一种预编码技术，允许发送方在不知道但假设了解干扰的情况下编码信息，从而达到信道容量。
7. 块对角几何均值分解（BD-GMD）：GMD的变种，适用于MIMO广播信道，将信道分解为SNR/SINR相同的子信道。
8. 块对角统一信道分解（BD-UCD）：BD-GMD的扩展，旨在实现MIMO广播信道的容量。
9. 信噪比（SNR）和信干比（SINR）：衡量通信系统中信号质量和干扰程度的指标。
10. 通信系统性能比较：通过数值模拟，BD-GMD和BD-UCD方案在性能上优于传统方法。
2780 IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS, VOL. 7, NO. 7, JULY 2008
Fig. 1. Block diagram of the MMSE-DFE scheme.
matrix X. Now, alternatively, the nulling and interference
matrices can be found via the QR-decomposition [3]
H
√
ηI
= Q
1
R
1
, Q
1
=
Q
1u
Q
1d
, R
1
= Λ
1
B
1
,
(5)
where Q
1
has orthonormal columns, Q
1u
is N
R
× N
T
, Q
1d
is N
T
× N
T
, R
1
is N
T
× N
T
and upper triangular, Λ
1
=
diag(R
1
),andB
1
is upper triangular with unit diagonal. (Note
that Q
1u
and Q
1d
are not unitary.) Then, the nu lling and
interference matrices satisfy
W
H
= Λ
−1
1
Q
H
1u
and B = B
1
. (6)
The symbols are detected from ˆx
N
T
to ˆx
1
as follows:
for i = N
T
: −1:1
ˆx
i
= C
[W
H
y]
i
−
N
T
j=i+1
[B]
i,j
ˆx
j
end
where C denotes the mapping to the nearest signal point in
the constellation. Ignoring the effect of error propagation, the
MMSE-DFE scheme produces decoupled subchannels of the
form y
i
= r
i
x
i
+ u
i
where r
i
is the i-th diagonal element of
Λ
1
.In[6],itwasshownthat
η(1 + ρ
i
)=r
2
i
, (7)
where ρ
i
is the SINR of the i-th subchannel. Thus, the capacity
of the scheme can be written as
N
T
i=1
log(1 + ρ
i
)=
N
T
i=1
log
r
2
i
η
=logdet
I +
1
η
H
H
H
.
(8)
This gives another proof that the MMSE-DFE receiver is
information lossless [16], [6].
B. MMSE-based DPC
One major problem with DFEs is error propagation. If CSI
is known at the transmitter, interference between subchannels
can be cancelled completely before transmission via DPC.
Here, a general view of MMSE-based DPC via successive
interference pre-subtraction is developed. Consider once again
the N
T
×N
R
point-to-point channel y = Hx+u from Section
II-A. However, it will not be required that E[uu
H
]=N
0
I
but only that E[|u
i
|
2
]=N
0
for each i. Assume that there
is n o collaboration between the receive antennas. Writing
h
ij
=[H]
i,j
,thei-th subchannel is
y
i
=(
j<i
h
ij
x
j
)+h
ii
x
i
+(
j>i
h
ij
x
j
)+u
i
. (9)
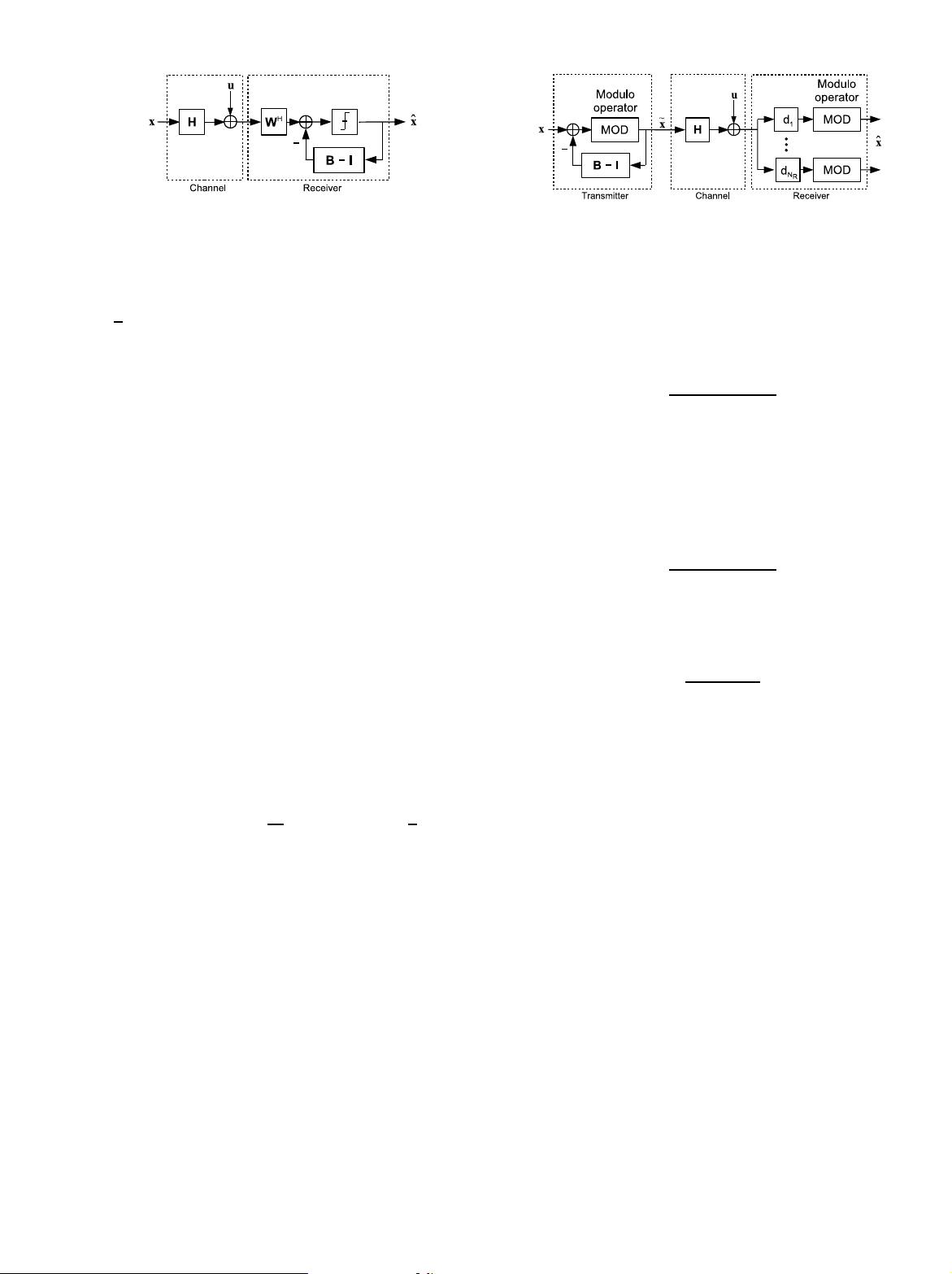
Fig. 2. Block diagram of the MMSE-DPC scheme using THP.
The hope is to treat (
j<i
h
ij
x
j
) as interference terms to
be cancelled at the transmitter. If these in terference terms are
cancelled perfectly, then a single input single output (SISO)
MMSE receiver that sees (
j>i
h
ij
x
j
)+u
i
as noise terms
can be used on each subchannel. The corresponding MMSE
coefficient for the i-th subchannel is
d
i
=
h
∗
ii
η +
j≥i
|h
ij
|
2
, (10)
where x
∗
is the conjugate of a complex number x. Denoting
D
d
= diag(d
1
,...,d
N
R
), the equivalent channel is now
D
d
H. Thus, the interference terms can be represented by the
lower triangular unit-diagonal matrix B = L(D
d
H), called
the interference matrix. Meanwhile, the SINR of the i-th
subchannel is given by
ρ
i
=
|h
ii
|
2
η +
j>i
|h
ij
|
2
. (11)
A simple and useful relation between (10) and (11) can be
noted at this point. Let Σ
0
= η +
j>i
|h
ij
|
2
. Then, ρ
i
=
|h
ii
|
2
/Σ
0
and d
i
= h
∗
ii
/(Σ
0
+ |h
ii
|
2
). Eliminating Σ
0
gives
d
i
=
ρ
i
h
ii
(1 + ρ
i
)
. (12)
One low-complexity suboptimal implementation of DPC is
Tomlinson-Harashima precoding (THP) [14]. The block di-
agram of a MMSE-based DPC scheme using THP is shown
in Figure 2. The vector ˜x to be transmitted can be evaluated
from ˜x
1
to ˜x
N
T
using
˜x
1
= x
1
for i =2:1:N
T
˜x
i
=mod
x
i
−
i−1
j=1
[B]
i,j
˜x
j
end
A downside of THP is the slight increase in the average
transmit power by a factor of M/(M − 1) for M -QAM
symbols, called the precoding loss. For large constellations,
this loss is negligible.
C. ZF-DPC
Consider the MIMO broadcast channel described in (1). If
CSI is available at the transmitter, interferenc e can cellation via
dirty paper precoding can be performed. THP can be used as a
suboptimal implementation of DPC. Conventional precoding
schemes often treat multiple antennas of different users as
different virtual users. One example is the zero-forcing THP
(ZF-THP) scheme [14]. It is based on the QR decomposition
H
H
= QR,orH = R
H
Q
H
. The linear precoder Q is
applied before transmission so that x = Qs,wheres is the
vector of information symbols to be sent. Th is transforms the
剩余11页未读，继续阅读
2020-06-07 上传
2022-09-24 上传
2022-07-14 上传
点击了解资源详情
2024-09-30 上传
2024-09-30 上传
2024-09-30 上传
qq_41391416
- 粉丝: 0
- 资源: 1
我的内容管理
展开
最新资源
- Aspose资源包：转PDF无水印学习工具
- Go语言控制台输入输出操作教程
- 红外遥控报警器原理及应用详解下载
- 控制卷筒纸侧面位置的先进装置技术解析
- 易语言加解密例程源码详解与实践
- SpringMVC客户管理系统：Hibernate与Bootstrap集成实践
- 深入理解JavaScript Set与WeakSet的使用
- 深入解析接收存储及发送装置的广播技术方法
- zyString模块1.0源码公开-易语言编程利器
- Android记分板UI设计：SimpleScoreboard的简洁与高效
- 量子网格列设置存储组件：开源解决方案
- 全面技术源码合集：CcVita Php Check v1.1
- 中军创易语言抢购软件：付款功能解析
- Python手动实现图像滤波教程
- MATLAB源代码实现基于DFT的量子传输分析
- 开源程序Hukoch.exe：简化食谱管理与导入功能
