MATLAB随机信号建模：Binornd与Normrnd函数应用解析

“基于MATLAB的随机信号及其参数建模分析.pdf”主要探讨了如何利用MATLAB进行随机信号的建模与分析，包括基本的随机信号概念以及如何使用MATLAB内置函数来生成和处理随机信号。文件中的示例主要涉及二项分布和正态分布的随机数生成。 在MATLAB中，`binornd`函数用于生成二项分布的随机数。二项分布描述了在n次独立的伯努利试验中成功次数的概率分布，其中每次试验的成功概率为p。在示例中，`binornd(10,0.5)`生成一个二项分布随机数，期望值为10，成功概率为0.5，结果可能为5。而`binornd(10,0.5,1,6)`生成6行1列的二维数组，每行代表一次试验的结果。其他例子展示了如何通过改变参数生成不同形状的二项分布随机数矩阵。 `normrnd`函数则用于生成正态分布的随机数。正态分布，也称为高斯分布，具有特定的均值和标准差。例如，`normrnd(1:6,1./(1:6))`生成均值从1到6，标准差分别为1/1,1/2,...,1/6的一维向量。`normrnd(0,1,[1,5])`生成一个1行5列的标准正态分布（均值0，标准差1）的矩阵。`normrnd([123;456],0.1,2,3)`生成一个2行3列的矩阵，其元素是均值为123或456，标准差为0.1的正态分布随机数。 此外，文件还提到了如何使用MATLAB计算正态分布和卡方分布的密度函数。例如，`pdf('norm',0.6578,0,1)`计算标准正态分布（均值0，标准差1）在点0.6578的密度函数值，结果为0.3213。而`pdf('chi2',2.18,8)`计算自由度为8的卡方分布，在点2.18的密度函数值，结果为0.0363。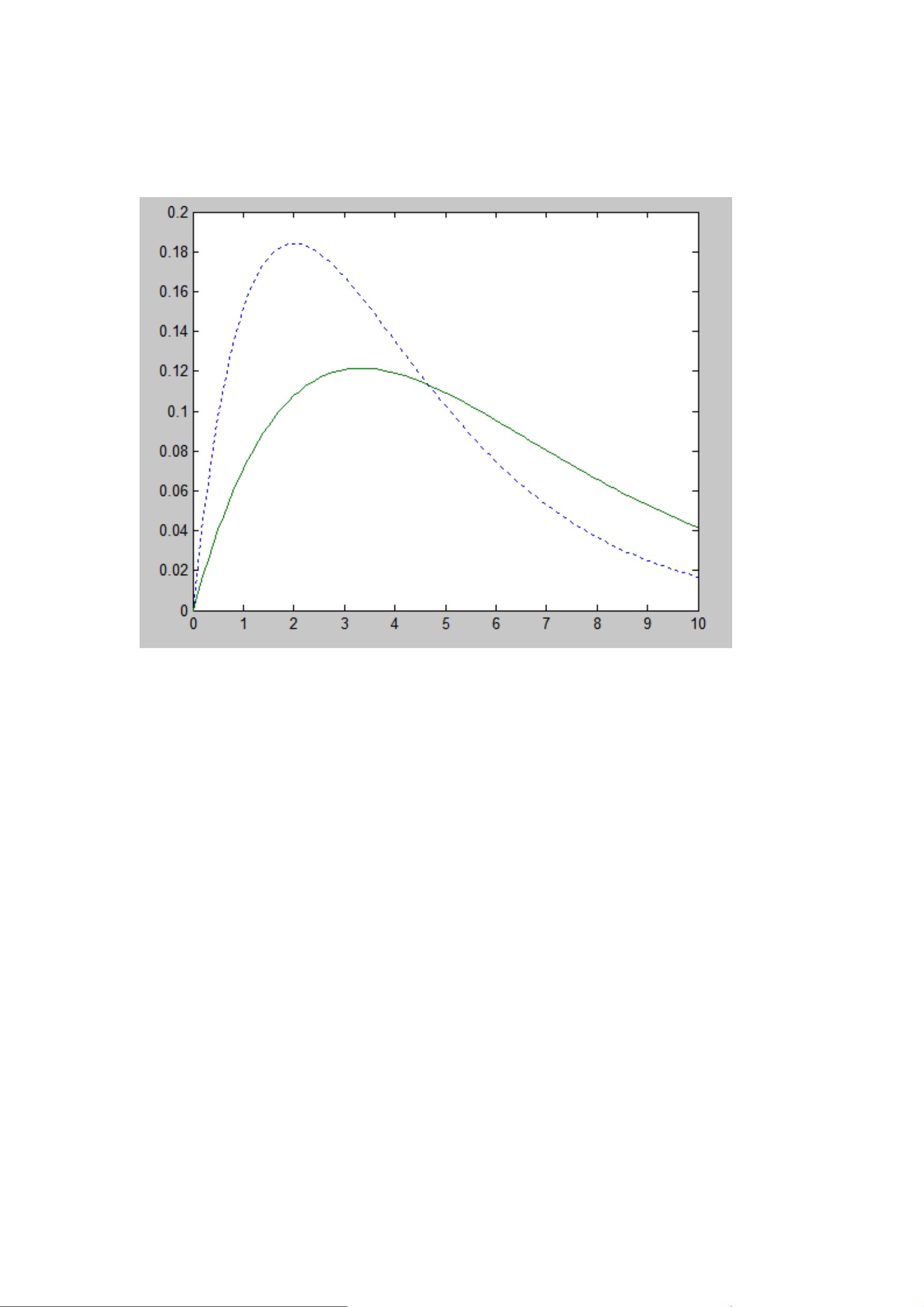 最后，文件还展示了如何绘制不同自由度的卡方分布密度函数图。`chi2pdf`函数用于计算卡方分布的密度函数，`plot`函数用于绘制图形。在示例中，`x=0:0.1:30`定义了x轴的取值范围，`y1=chi2pdf(x,2)`和`y2=chi2pdf(x,6)`分别计算了自由度为2和6时的密度函数，然后用不同的标记样式绘制在图上。 这些内容对于理解MATLAB中的随机信号建模和分析，以及掌握概率分布的生成和性质是非常重要的。通过学习和实践，用户可以有效地模拟和研究各种随机过程，这对于通信系统、控制系统、信号处理等领域具有广泛的应用价值。