Matlab基础入门：矩阵操作与复数详解

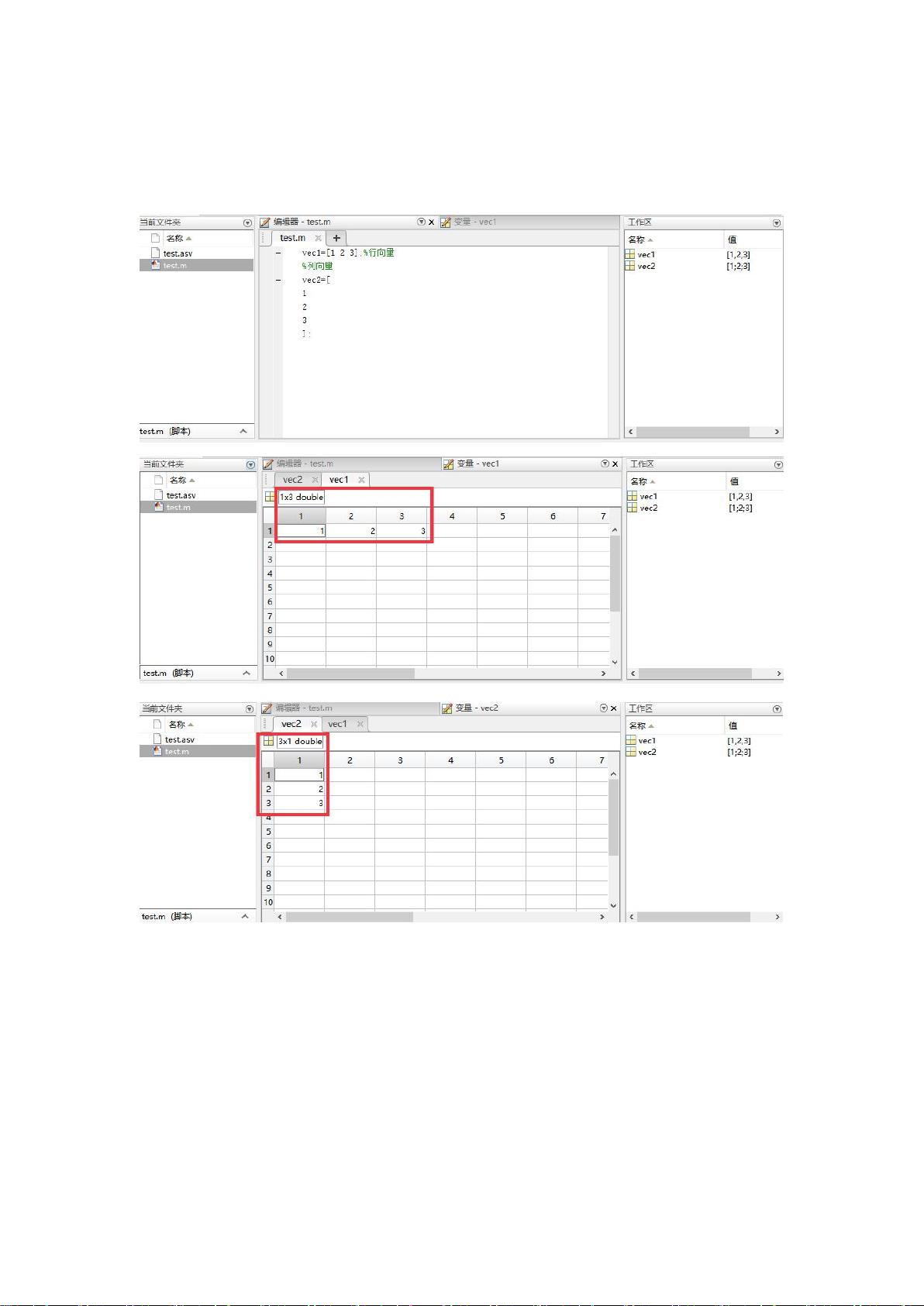
MATLAB是一种广泛应用于工程、科学计算和数据分析领域的高级编程环境，以其直观易用的矩阵操作和可视化功能而闻名。本篇文档旨在为初学者提供一个基础的MATLAB教程，帮助快速理解和掌握核心概念。 首先，我们了解如何创建和处理基本的数据结构。MATLAB中的向量和矩阵是数据的主要载体。向量在MATLAB中被视为一维数组，可以通过输入连续的数值，如`[1 2 3]`来创建，也可以用行或列向量形式表示。矩阵则是二维数组，如`[1 2; 3 4]`，其中分号用来区分行。此外，MATLAB还提供了诸如`zeros()`、`ones()`和`eye()`等函数，用于创建全零矩阵、全一矩阵和对角线元素为1的单位矩阵。 矩阵运算是MATLAB的核心功能之一。其中包括基本的算术运算（如数乘，`*`操作符），对矩阵元素逐个执行。需要注意的是，数乘（点乘）与普通的乘法运算不同，后者通常指的是矩阵乘法（`*`），涉及到矩阵维度的匹配。另外，矩阵的转秩（转置）在MATLAB中通过'符号实现，`A.'会返回矩阵A的转置。求逆（逆矩阵）则通过`inv()`函数完成，如`inv(A)`，其结果是A的逆，满足`A * inv(A) = eye(size(A))`。 点积（内积）是另一个关键运算，它要求参与运算的两个矩阵具有相同的行数和列数，通过元素逐对应相乘然后求和得到。矩阵拼接则有扩展维度（`[A B]`）和保持维度（`[A; B]`）两种方式，分别表示水平拼接和垂直拼接。 复数在MATLAB中也很常见，可以用实部和虚部的形式表示，如`3 + 4i`或`3 + j*4`，虚数单位`i`或`j`在表达式中被支持。 对于矩阵元素的引用，MATLAB采用的是1-based indexing，即元素下标从1开始，如`A(1,1)`表示第一行第一列的元素。多元素引用可以通过逗号分隔，如`A(1:3, 2:4)`选取第1到第3行，第2到第4列的子矩阵。 最后，MATLAB重视工作区数据管理。`whos`命令用于查看当前工作区中变量的名称、大小和类型，`save`命令用于保存工作区的数据，格式为`.mat`，而`load`命令则用于加载已保存的数据，数据会被以结构体的形式导入，引用时需注意字段名与变量名的一致性。 掌握这些MATLAB基础知识是学习更高级应用和算法开发的基础，通过实践操作和反复练习，能够有效提升在MATLAB中的编程技能。