iOS开发：深入探索AVFoundation框架

需积分: 10 148 浏览量更新于2024-07-18 收藏 9.38MB PDF 举报

"iOS avfoundation框架详解，包括视频和音频开发，附带多个示例" 在iOS平台上，多媒体处理是一个至关重要的领域，而苹果提供的AVFoundation框架则是实现这一目标的核心工具。AVFoundation是一个全面且强大的框架，它允许开发者处理音频、视频、图像以及时间线编辑等多种媒体任务。本资源详细介绍了如何在iOS应用中使用AVFoundation进行视频和音频的开发。首先，AVFoundation框架的出现是为了解决QuickTime框架的局限性。QuickTime虽然历史悠久，但在2000年代中期，由于技术的快速发展，其结构和功能已经显得过时，如旧的编程习惯、对不再流行系统API的依赖，以及一些不再适用的功能。随着CPU架构的转变（从 Motorola 68000 系列到 PowerPC，再到 Intel x86），QuickTime的更新和维护变得复杂且难以理解。苹果在新千年初期的一系列不完整的更新，比如在Java和Objective-C中的QTKit，预示着他们正在规划新的多媒体解决方案。随着iPhone的发布，苹果推出了AVFoundation框架，它为iOS设备提供了更好的媒体支持。最初的iOS SDK虽然在媒体支持方面比较有限，但随着AVFoundation的发展，开发者可以实现更多高级功能，如播放、录制、编辑和处理音频和视频流。该框架包括了AVFoundation的核心组件，如AVPlayer、AVPlayerItem、AVAsset、AVAudioPlayer等，它们分别用于播放媒体、管理播放列表、加载和操作媒体资源以及处理音频播放。 AVPlayer和AVPlayerItem是AVFoundation中的关键类，用于播放音频和视频。AVPlayer可以加载一个AVPlayerItem，后者包含了具体的媒体资源信息。通过设置AVPlayer的代理，开发者可以监听播放状态、进度变化和其他事件。同时，AVAsset类提供了一种抽象的方式来访问和控制多媒体内容，包括元数据、音轨、视频轨道等。在音频处理方面，AVAudioEngine是AVFoundation的重要组成部分，它允许开发者创建复杂的音频处理图，包括录音、混音和实时音频处理。AVAudioPlayer类则简化了单个音频文件的播放，适合简单的背景音乐或音效。此外，AVFoundation还支持视频编码和解码，这得益于AVAssetExportSession和AVAssetReader/AVAssetWriter等类。开发者可以利用这些工具进行视频转码、提取音频流或者添加水印等操作。对于更底层的视频处理，如硬件加速解码和编码，可以借助VideoToolbox框架，它提供了与硬件更直接的交互。在实际开发中，这个资源中提到的"很多demo"将帮助开发者理解并实践AVFoundation的各种功能。通过这些示例，开发者可以学习如何初始化和控制播放器，处理视频和音频流，以及如何进行多媒体内容的导入和导出。AVFoundation是iOS开发者的强大工具，它使得在移动设备上创建丰富的多媒体体验成为可能。

Figure 1.3 Audio signal voltage

Returning to the topic of sampling, how do we convert this continuous signal into its discrete form? Let’s drill in a

bit further into the essential element in an audio signal. Using a tone generator, I created two different tones pro-

ducing the sine waves shown in

Figure 1.4.

Figure 1.4 Sine waves at 1Hz (left) and 5Hz (right)

We’re interested in two aspects of this signal. The first is the amplitude, which indicates the magnitude of the volt-

age or relative strength of the signal. This can be represented on a variety of scales, but is commonly normalized to

a range of –1.0f to 1.0f. The other interesting aspect of this signal is its frequency. The frequency of the signal is

measured in hertz (Hz), which indicates how many complete cycles occur in the period of one second. The image

on the left in

Figure 1.4 shows an audio signal cycling at 1Hz and the one on the right shows a 5Hz signal. Humans

have an audible frequency range of 20Hz–20kHz (20,000 Hz), so both signals would be inaudible, but they make

for easier illustration.

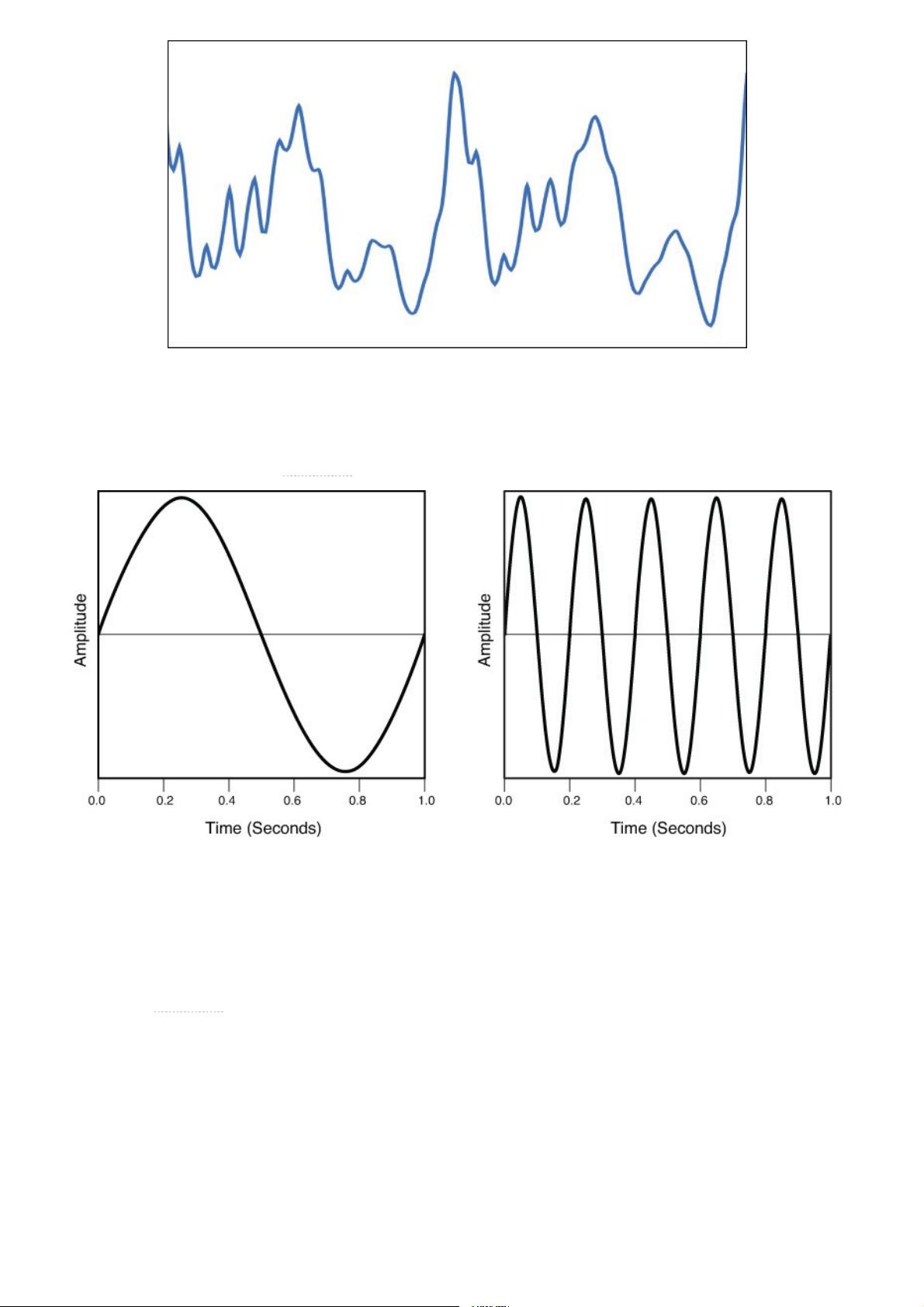
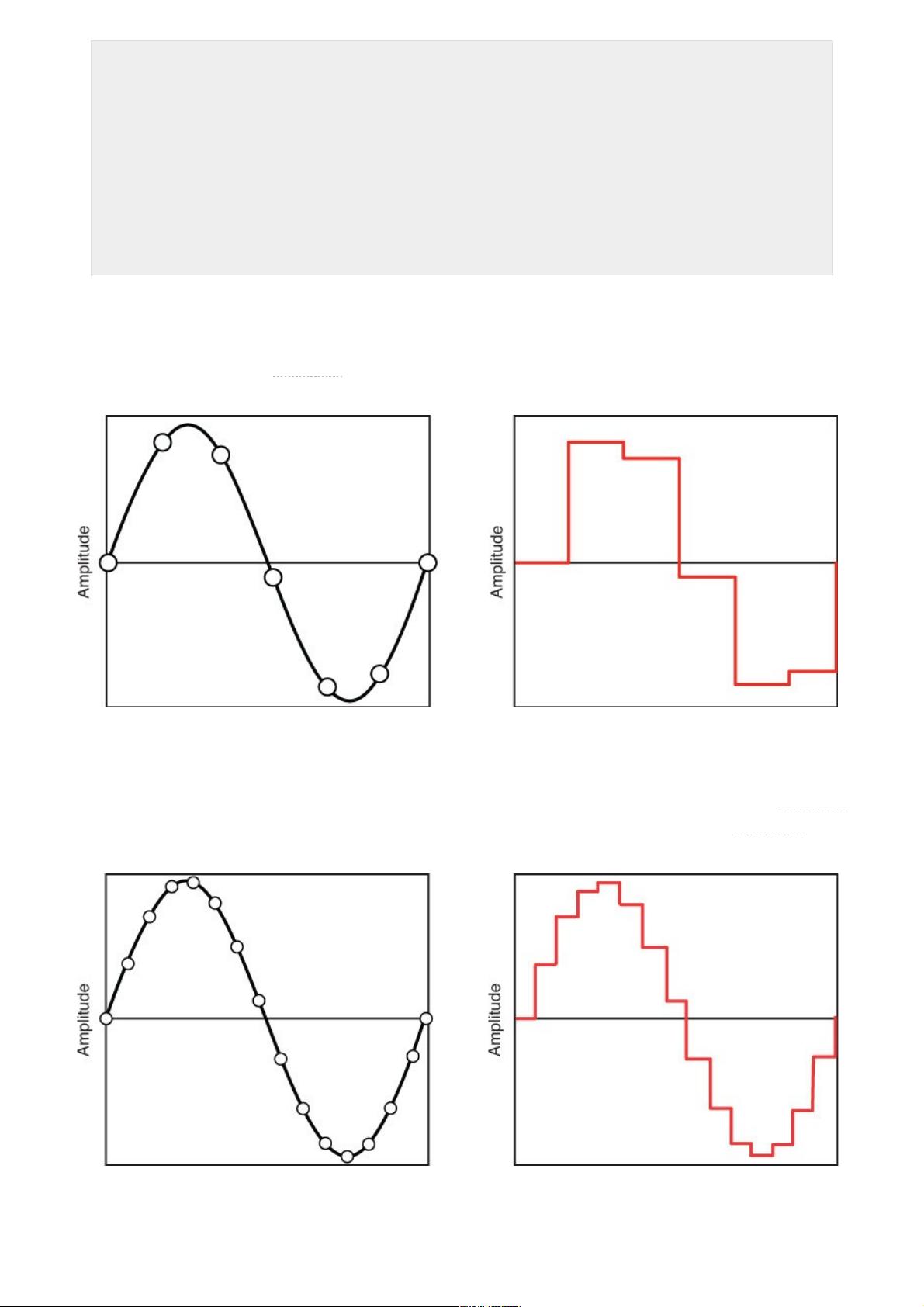
surmise from this example is if you continue to increase the frequency of the sample rate, we should be able to

produce a digital representation that fairly accurately mirrors the original source. Given the limitations of hard-

ware, we may not be able to produce an exact replica, but is there a sample rate that can produce a digital repre-

sentation that is good enough? The answer is yes, and it’s called the Nyquist rate. Harry Nyquist was an engineer

working for Bell Labs in the 1930s who discovered that to accurately capture a particular frequency, you need to

sample at a rate of at least twice the rate of the highest frequency. For instance, if the highest frequency in the au-

dio material you wanted to capture is 10kHz, you need a sample rate of at least 20kHz to provide an accurate digi-

tal representation. CD-quality audio uses a sampling rate of 44.1kHz, which means that it can capture a maximum

frequency of 22.05kHz, which is just above 20kHz upper bound of human hearing. A sampling rate of 44.1kHz

may not capture the complete frequency range contained in the source material, meaning your dog may be upset

by the recording because it doesn’t capture the nuances of the Abbey Road sessions, but for us human beings, it

sounds pristine.

In addition to the sampling rate, another important aspect of digital audio sampling is how accurately we can cap-

ture each audio sample. The amplitude is measured on a linear scale, hence the term Linear PCM. The number of

bits used to store the sample value defines the number of discrete steps available on this linear scale and is re-

ferred to as the audio’s bit depth. Assigning too few bits results in considerable rounding or quantizing of each

sample, leading to noise and distortion in the digital audio signal. Using a bit depth of 8 would provide 256 dis-

crete levels of quantization. This may be sufficient for some audio material, but it isn’t high enough for most audio

content. CD-quality audio has a bit depth of 16, resulting in 65,536 discrete levels, and in professional audio

recording environments bit depths of 24 or higher are used.

When we digitize a signal, we are left with its raw, uncompressed digital representation. This is the media’s purest

digital form, but it requires significant storage space. For instance, a 44.1kHz, 16-bit LPCM audio file takes about

10MB per stereo minute. To digitize a 12-song album with the average song length of 5 minutes would take approx-

imately 600MB of storage. Even with the vast amounts of storage and bandwidth we have today, that is still pretty

large. We can see that uncompressed digital audio requires significant amounts of storage, but what about uncom-

pressed video? Let’s take a look at the elements of a digital video to see if we can determine the amount of storage

space it requires.

Video is composed of a sequence of images called frames. Each frame captures a scene for a point in time within

the video’s timeline. To create the illusion of motion, we need to see a certain number of frames played in fast suc-

cession. The number of frames displayed in one second is called video’s frame rate and is measured in frames per

second (FPS). Some of the most common frame rates are 24FPS, 25FPS, and 30FPS.

To understand the storage requirements for uncompressed video content, we first need to determine how big each

individual frame would be. A variety of common video sizes exist, but these days they usually have an aspect ratio

of 16:9, meaning there are 16 horizontal pixels for every 9 vertical pixels. The two most common sizes of this as-

pect ratio are 1280 × 720 and 1920 × 1080. What about the pixels themselves? If we were to represent each pixel

in the RGB color space using 8 bits, that means we’d have 8 bits for red, 8 bits for green, and 8 bits for blue, or 24

bits. With all the inputs gathered, let’s perform some calculations.

Table 1.1 shows the storage requirements for un-

compressed video at 30FPS at the two most common resolutions.

Table 1.1 Uncompressed Video Storage Requirements

Houston, we have a problem. Clearly, as a storage and transmission format, this would be untenable. A decade

from now these sizes may seem trivial, but today this isn’t feasible for most uses. Because this isn’t a reasonable

way to store and transfer video in most cases, we need to find way to reduce this size. This brings us to the topic of

compression.

Digital Media Compression

To reduce the size of digital media we need to use compression. Virtually all the media we consume is compressed

to various degrees. Whether it’s video on TV, a Blu-ray disc, streamed over the web, or purchased from the iTunes

Store, we’re dealing with compressed formats. Compressing digital media can result in greatly reduced file sizes,

but often with little or no perceivable degradation in quality.

Chroma Subsampling

Video data is typically encoded using a color model called YCC,—which is commonly referred to as YUV. The

term YUV is technically incorrect, but YUV probably rolls off the tongue better than Y-Prime-C-B-C-R. Most soft-

ware developers are more familiar with the RGB color model, where every pixel is composed of some value of red,

green, and blue. Y’C C , or YUV, instead separates a pixel’s luma channel Y (brightness) from its chroma (color)

channels UV.

Figure 1.7 illustrates the effect of separating an image’s luma and chroma channels.

Figure 1.7 Original image on the left. Luma (Y) in the center. Chroma (UV) on the right.

You can see that all the detail of the image is preserved in the luma channel, leaving us with a grayscale image,

whereas in the combined chroma channels almost all the detail is lost. Because our eyes are far more sensitive to

brightness than they are to color, clever engineers over the years realized we can reduce the amount of color infor-

mation stored for each pixel while still preserving the quality of the image. The process used to reduce the color

data is called chroma subsampling.

Whenever you see camera specifications or other video hardware or software referring to numbers such as 4:4:4,

4:2:2, or 4:2:0, these values refer to the chroma subsampling it uses. These values express a ratio of luminance to

chrominance in the form J:a:b where

J: is the number of pixels contained within some reference block (usually 4).

a: is number of chrominance pixels that are stored for every J pixels in the first row.

b: is the number of additional pixels that are stored for every J pixels in the second row.

To preserve the quality of the image, every pixel needs to have its own luma value, but it does not need to have its

own chroma value.

Figure 1.8 shows the common subsampling ratios and the effects of each.

Figure 1.8 Common chroma subsampling ratios

In all forms, full luminance is preserved across all pixels, and in 4:4:4 full color information is preserved as well.

In 4:2:2, color information is averaged across every two pixels horizontally, resulting in a 2:1 luma-to-chroma ra-

tio. In 4:2:0, color information is averaged both horizontally and vertically, resulting in a 4:1 luma-to-chroma ratio.

Chroma subsampling typically happens at the point of acquisition. Some professional cameras capture at 4:4:4, but

more commonly they do so at 4:2:2. Consumer-oriented cameras, such as the one found on the iPhone, capture at

4:2:0. A high-quality image can be captured even at significant levels of subsampling, as is evidenced by the quality

of video that can be shot on the iPhone. The loss of color becomes more problematic when performing chroma

keying or color correction in the post-production process. As the chroma information is averaged across multiple

pixels, noise and other artifacts can enter into the image.

Codec Compression

Most audio and video is compressed with the use of a codec, which is short for encoder/decoder. A codec is used to

encode audio or video data using advanced compression algorithms to greatly reduce the size needed to store or

deliver digital media. The codec is also used to decode the media from its compressed state into one suitable for

playback or editing.

Codecs can be either lossless or lossy. A lossless codec compresses the media in a way that it can be perfectly re-

constructed upon decompression, making it ideal for editing and production uses, as well as for archiving pur-

poses. We use this type of compression frequently when using utilities like zip or gzip. A lossy codec, as the name

suggests, loses data as part of the compression process. Codecs employing this form of compression use advanced

algorithms based on human perception. For instance, although we can theoretically hear frequencies between

20Hz and 20kHz, we are particularly sensitive to frequencies between 1kHz and 5kHz. Our sensitivity to the fre-

quencies begins to taper off as we get above or below this range. Using this knowledge, an audio codec can employ

filtering techniques to reduce or eliminate certain frequencies in an audio file. This is just one example of the many

approaches used, but the goal of lossy codecs is to use psycho-acoustic or psycho-visual models to reduce redun-

dancies in the media in a way that will result in little or no perceivable degradation in quality.

Let’s look at the codec support provided by AV Foundation.

剩余328页未读，继续阅读

sagesong

粉丝: 0
资源: 5

iOS开发：深入探索AVFoundation框架

高清彩版 IOS AVFoundation 秘籍

苹果cms手机版影院视频网站源码.zip_seasonafy_影视_苹果CMSa片电影_苹果cmsa大片_苹果cmsa影院

IOS利用AVFoundation框架实现录音和播放 (AVAudioSession AVAudioRecorder AVAudioPlayer)

ios AVFoundation

iOS AVFoundation

ios-iOS AVFoundation实现二维码的扫描、识别.zip

掌握iOS AVFoundation实现视频裁剪技巧

IOS AVFoundation面试题

深入解析iOS AVFoundation框架在百度地图毕业设计中的应用

iOS使用AVFoundation展示视频

最新资源