编程实现Mallat快速小波变换：详解与MATLAB示例

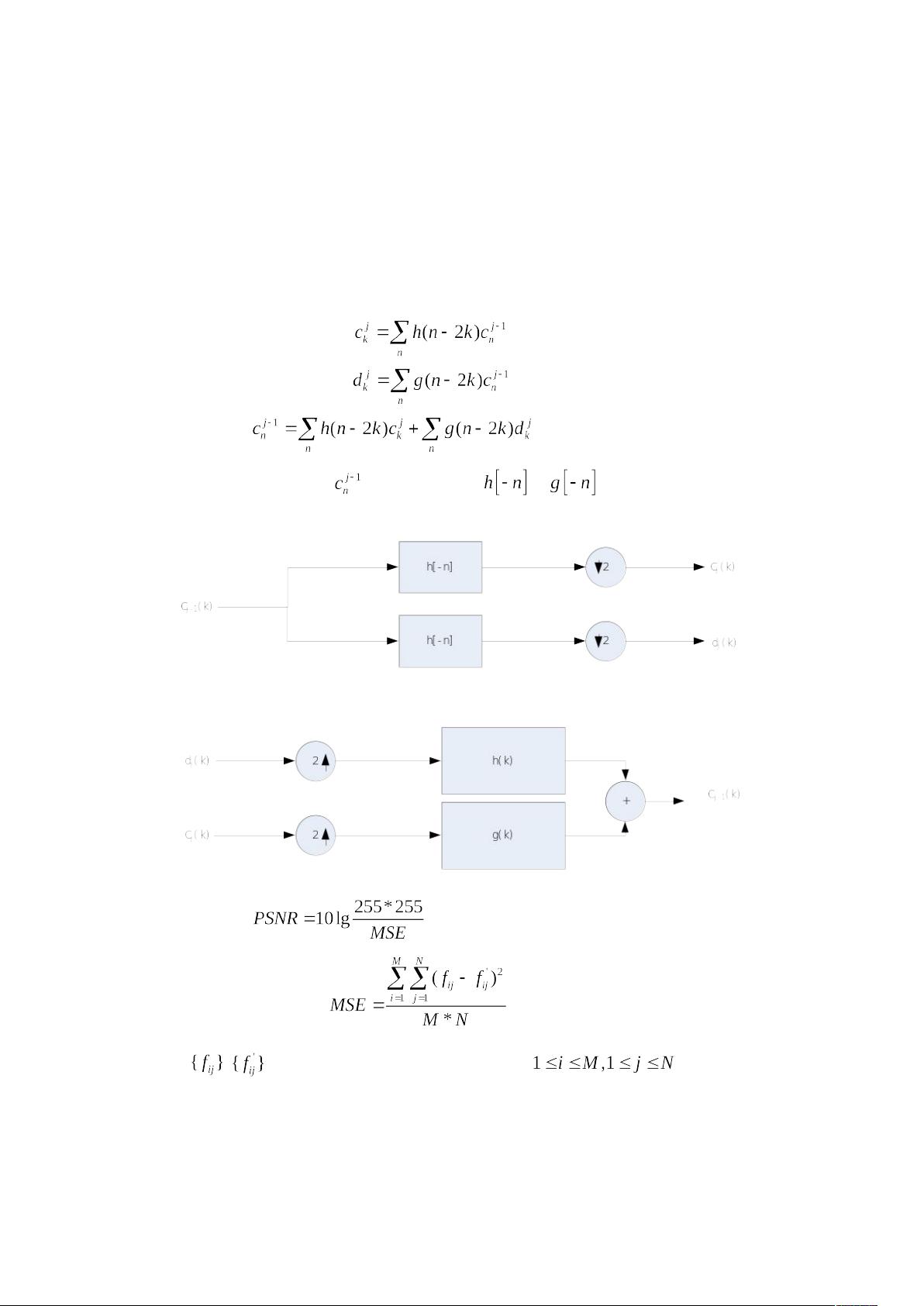
小波变换是一种强大的信号处理工具，尤其在数据分析和图像处理中有着广泛应用。在这个实验中，我们将深入探讨离散快速小波变换的Mallat算法，并通过Matlab编程来实现这一过程。 首先，实验的目标是通过编程实践，增强对二维小波变换的理解，提升编程技能，并熟悉Matlab在实际问题中的应用。Mallat算法是一种高效的小波分解方法，它利用递归结构和“抽取”操作，将信号分解成低频和高频两部分，便于分析和特征提取。 算法的核心是基于两个滤波器，一个称为低通滤波器h，另一个为高通滤波器g。这两个滤波器通过与输入信号进行卷积操作，得到下一级的低频和高频系数。在实验中，原始图像首先进行边界延拓，这涉及到不同的延拓方法，如零延拓、周期延拓、对称周期延拓和常数连续延拓，以确保变换的正确性。 分解阶段的编程思路采用了循环结构，通过逐个元素的相乘和累加，计算出低频系数r1和高频系数r2。具体来说，对于每个像素，先计算h和x的卷积，然后将结果保存到相应的矩阵中。同样的过程也应用于g和x。最后，这些系数形成了一维向量y，存储了整个图像的分解结果。 重构阶段则是逆过程，通过快速傅里叶变换（FFT）和反快速傅里叶变换（IFFT），结合低频和高频系数，恢复原始图像。在这个过程中，为了减少计算复杂性，使用频域相乘来代替时域的卷积操作。 这个实验不仅涉及小波变换的基本理论，还包括了Matlab编程的实际应用，学生将在实践中学习如何设计和实现小波分解，以及如何处理边界条件，这对于理解和掌握小波变换技术至关重要。完成这个项目后，参与者将具备在图像处理和信号分析中使用小波变换的能力，为后续深入学习打下坚实的基础。