"快速傅里叶变换（FFT）：高效计算DFT的算法"

快速傅里叶变换（FFT）是一种计算离散傅里叶变换（DFT）的快速高效算法。在数字技术中，有限长序列的频谱可以被离散化，因此有限长序列的DFT可以完整地表示序列的频谱，从而可以直接对信号进行频谱分析。谱分析在通信技术、图像传输、语音压缩、生物医学等领域有很多应用。 尽管频谱分析和DFT运算非常重要，但由于DFT运算量过大，很长一段时间以来并没有真正得到应用，频谱分析大多使用模拟信号滤波的方法来解决。直到1965年，美国IBM公司的库利和图基科学家提出DFT运算的一种快速算法，情况才发生了根本性变化。人们开始认识到DFT运算的一些内在规律，并快速发展和完善了一套高速有效的运算方法，也就是现在我们熟知的快速傅里叶变换（FFT）算法。FFT的出现大大简化了DFT的运算，使运算时间缩短了1-2个数量级，从而使DFT在实际应用中得到广泛应用。 在进行一次DFT运算时，有限长序列x(n)需要进行的运算量是一个重要的特点。一般来说，序列x(n)和DFT的长度N成正比例关系。对于长度为N的序列，进行一次DFT运算所需的运算量是O(N^2)。这意味着当序列长度增长时，DFT运算的计算量会成倍增加，导致计算时间大幅增加。在实际应用中，对于大规模的信号和数据进行频谱分析，传统的DFT计算是不切实际的。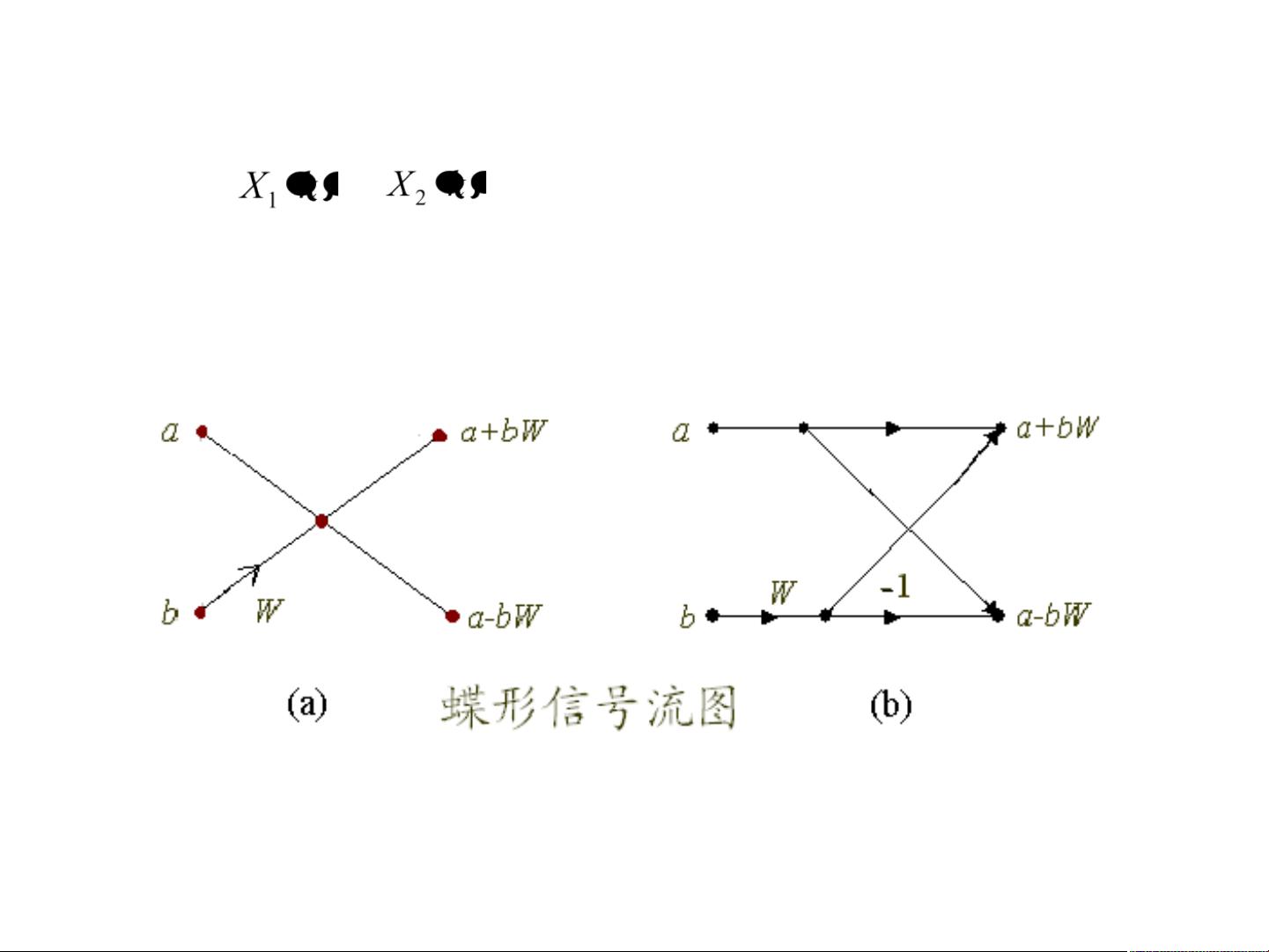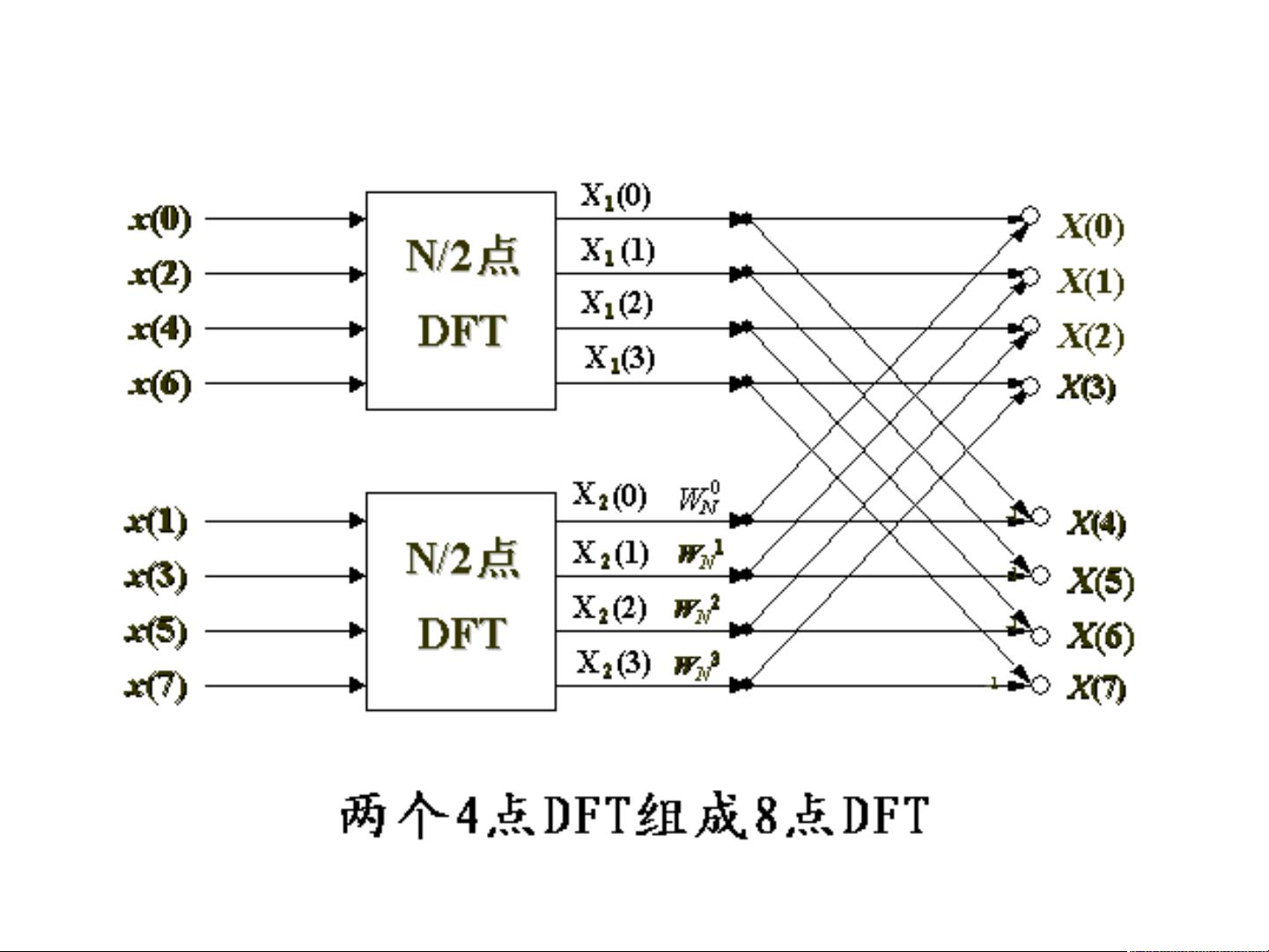 为了解决这个问题，FFT算法应运而生。FFT算法通过利用DFT运算的对称性质和重叠子问题的特点，将DFT计算拆分成多个较小规模的DFT计算，从而大大减少了运算量。FFT算法的时间复杂度仅为O(NlogN)，远远低于传统的DFT计算。通过使用FFT算法，可以在同样的计算时间内处理更大规模的信号和数据，实现实时频谱分析和处理。 FFT算法已经被广泛应用于许多领域。在通信技术中，FFT常用于信号的调制解调、频谱分析和信号处理。在图像传输领域，FFT被用于图像的压缩和解压缩等方面。在语音压缩和语音识别领域，FFT常用于信号的频谱分析和特征提取。在生物医学领域，FFT常用于医学图像处理和信号分析，如磁共振成像（MRI）中的图像重建和心电图（ECG）中的心率分析。 总之，快速傅里叶变换（FFT）是一种快速高效的计算离散傅里叶变换（DFT）的算法。它的出现极大地简化了DFT的运算，减少了运算量，从而使DFT在实际应用中得到广泛应用。FFT算法已经在通信技术、图像传输、语音压缩和生物医学等领域发挥着重要的作用，使频谱分析和信号处理变得更加高效和实时。