Loop细分模型的边界拼接算法实现无缝拼合

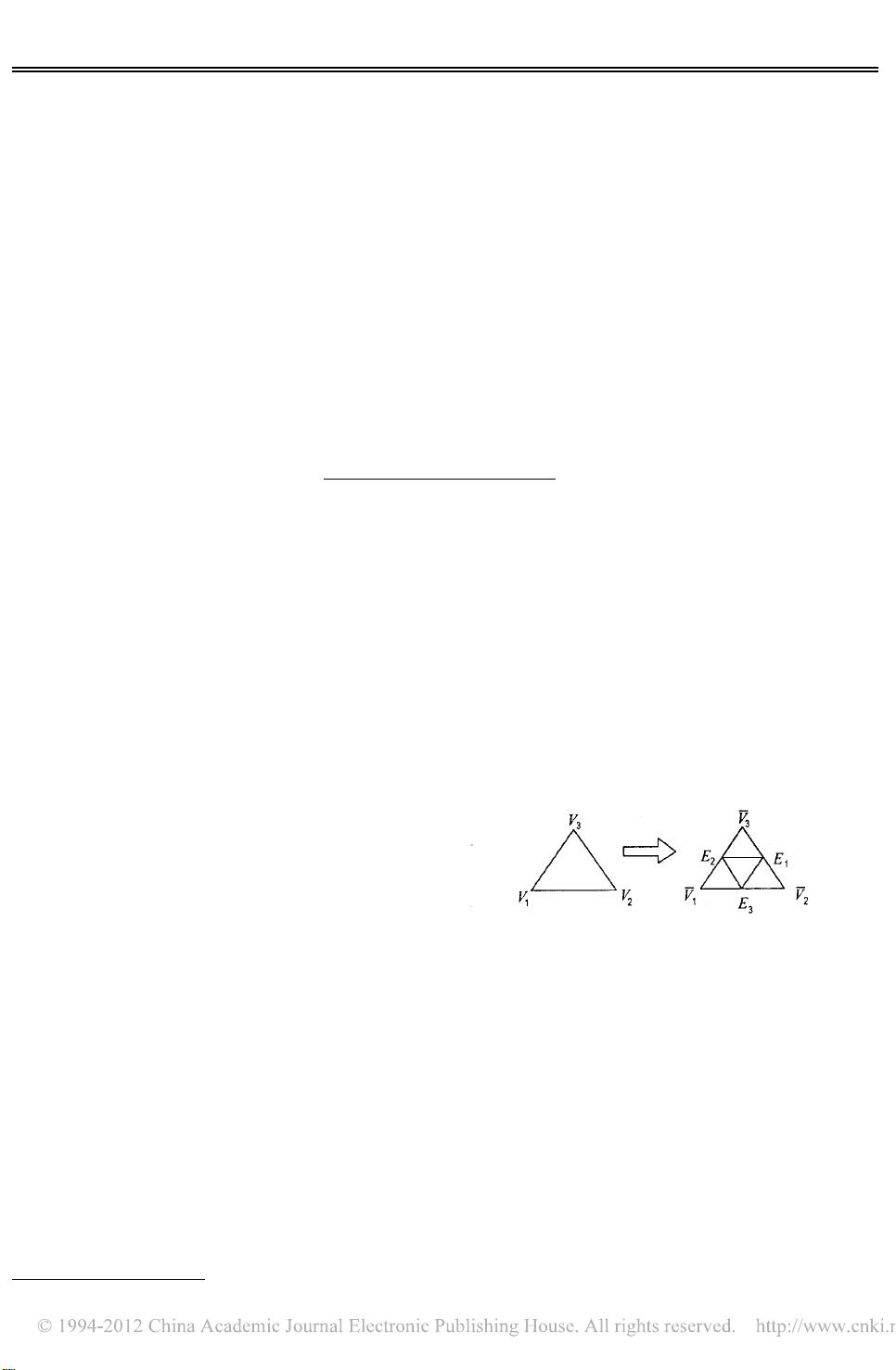
"该文主要讨论了LOOP细分模型的边界拼接算法，旨在解决细分曲面之间的光滑拼接问题。通过提出一种满足边界条件的Loop细分算法，可以在两个细分模型的拼接处实现C2连续性，而在边界奇异点达到C1连续性。文中还提到了细分方法的发展，如Catmull-Clark和Doo-Sabin细分模式，并指出Loop细分模式在非奇异点的C2连续性和奇异点的C1连续性。作者们探讨了细分曲面拼接的挑战，尤其是如何确保拼接的光滑度，并引用了Levin的工作作为相关背景。" Loop细分模型是一种基于三角网格的曲面细分技术，它扩展了箱式样条曲面的概念。在细分过程中，Loop算法通过在现有网格上插入新顶点并迭代这个过程，来逐渐提高曲面的质量和细节。与其他细分模式（如Catmull-Clark和Doo-Sabin）类似，Loop细分适用于具有不同拓扑结构的网格，但其优势在于能够在非奇异点实现C2连续性，这意味着曲面在这些点上的切线、法线和曲率都连续，提供了更平滑的过渡。 然而，在边界处，Loop细分模型可能会出现奇异点，这些点只能达到C1连续性，即切线连续但法线和曲率可能不连续。为了解决这个问题，文章提出了一个新的边界拼接算法，该算法特别考虑了边界条件，使得两个细分模型在拼接时不仅保持内部的C2连续性，而且在边界奇异点也能实现C1连续，从而改善整体的视觉效果和几何精度。 在实际应用中，如计算机图形学、产品设计和动画等领域，细分曲面的拼接是至关重要的，因为它允许模型的无缝集成和复杂形状的构建。Levin的工作为满足边界条件的细分曲面拼接提供了一种方法，但该文的贡献在于提出了一种适用于LOOP细分模型的特定解决方案，这有助于在拼接过程中维持更高的光滑度和精确性。 这篇研究论文对细分模型的边界拼接问题进行了深入探讨，提供了新的算法思路，对于提升细分模型在图形学中的应用质量和效率具有积极意义。通过这种技术，设计师和工程师可以创建更真实、更精细的3D模型，同时减少由于拼接不连续性带来的视觉干扰。