空中目标跟踪技术综述：动态模型分析

需积分: 44 6 浏览量更新于2024-07-21 3 收藏 4.97MB PDF 举报

"空中目标检测与跟踪：一项对X. RONG LI和VESSELIN P. JILKOV研究成果的综合调查" 这篇论文是关于空中目标跟踪技术的全面且最新的研究综述，特别关注在不考虑所谓测量源不确定性的情况下，如何追踪机动目标。由X. RONG LI和VESSELIN P. JILKOV两位IEEE会员共同完成，来自新奥尔良大学。论文分为多个部分，深入探讨了不同类型的机动目标运动/动力学模型。第一部分，引言，介绍了研究的背景和目标，为读者概述了整个领域的重要性和当前的技术挑战。第二部分，数学模型在机动目标跟踪中的应用，详细阐述了用于机动目标跟踪的各种数学模型，这些模型是理论研究和实际应用的基础。第三部分，非机动模型，讨论了适用于非机动目标的传统跟踪模型，这些模型在简单线性运动情况下表现良好，但可能无法准确描述复杂或突然变化的机动行为。第四部分，坐标非耦合机动模型，介绍了一种特殊的方法，它允许在不同的坐标系下独立处理目标的各个运动分量，提高了模型的灵活性和准确性。第五部分，二维水平运动模型，专注于平面内的目标运动，这种模型常用于分析地面或低空飞行的目标。第六部分，三维运动模型，则更进一步，考虑了目标在空间中的完整运动轨迹，适用于高空飞行器或卫星的跟踪。第七部分，结论性评论，总结了各种模型的优缺点，提供了模型之间关系的见解，并对未来的研究方向提出了建议。这篇论文的提交日期为2002年9月11日，经过修订后于2003年4月22日最终确定，同年7月31日发布，是IEEE Transactions on Aerospace and Electronic Systems期刊的一部分，编号为T-AES/39/4/822061。该研究对于理解和改进空中目标跟踪算法，特别是在处理高机动目标时，具有重要的理论价值和实践指导意义。通过对各种模型的比较和分析，研究人员和工程师可以更好地选择适合特定应用场景的跟踪策略。

where

(

)=(

@=@!

)

(

)

. If (66) is

used, howe ver, these models have an identical state

prediction because

[

(

)

(

)

(70)

where

stands for all measurements through time

. This follows from

[

, a consequence of (66). Nevertheless,

the corresponding covariances differ because different

models are used. That is why these models result

in very similar tracking performance, as reported

in [72] without explanation, for two IMM-EKF

(interacting multiple model) algorithms using the first

two schemes above with real ATC data. The state

prediction would also be different if model (68) is

used.

We point out that it is theoretically more appealing

to obtain a discrete-time model for state vector

]



by discretizing the following

continuous-time equations

jointly

[

]



(

)=(



)



(

) (71)

(



®!

(

) (72)

where

=0or 1

=¿

. It is reasonable to expect an

improvement in performance with this alternative at

the price of an increased complexity.

A continuous-time model is more accurate

than its discrete-time versions, but the latter are

needed for most applications. In the case where

the continuous-time model is nonlinear, such as

the CT models with unknown turn rate, there are

in general at least two approaches to acquiring its

discrete-time linear approximate models. Such models

are needed in the application of a linear (e.g., Kalman)

filter based nonlinear filtering technique. The first

is to linearize the nonlinear equation for the state

first and then discretize the linearized differential

equation (by finding the solution via integration).

This approach is more commonly used because it

is easy. An alternati ve is to discretize the nonlinear

state-space equation first and then linearize the

discrete-time model. These two approaches are

referred to as

discretized linearization

and

linearized

discretization

, respectively, in [73, 64]. The second

approach appears more accurate in general than the

first since linearization usually lose more accuracy

than discretization and thus should be done later.

However, the second approach may not be tractable

in general because discretization requires solving

the nonlinear dif ferential equation, which is often a

great challenge. Fortunately , for the CT motion with

an unknown turn rate, the corresponding differential

equations for the state are simple and the solution

can be readily obtained [73, 64]. The equations of the

nearly CT model, obtained by the first approach, and

some performance comparison results are also gi ven

in [73, 64].

As stated before, the choice of the state vector is

not trivial for the turn models. Essentially two classes

have been proposed. They differ in the representation

of the velocity vector: in the Cartesian and polar

coordinates, respectively.

CT Models with Cartesian Velocity

:In

this model, the state vector is chosen to be

[

]



; that is, the velocity vector (

)



is represented in the Cartesian coordinates.

Consequently, a direct discrete-time version of the

model is given by (see [67, 2]):



(





+diag[

,1]

(73)

where



®T



, or something

similar,

was given in (14),

]



zero-mean white noise with suitable statistics—they

are noise terms for acceleration in the

and

directions and for turn rate.

This model is known to be used successfully

as one of models in numerous multiple-model

configurations (see, e.g., [74, 67, 2, 75, 4]).

CT Models with Polar Velocity

: Obviously, the

velocity vector can also be represented in the polar

coordinates as [

]



in terms of speed

and (velocity) heading angle

=tan



(

). The state

vector is thus

]



. The corresponding

differential equation is given by (5) with

(

[

cos

sin

,0,

,0]



;thatis

(

)=[

cos

sin

,0,

,0]



(

) (74)

which follows immediately from (57)–(60) by setting

and

constant. By linearization first and then

discretization, its discrete-time linearized model is

given in [76] (see also [1]):







+(2

)

sin(

!T=

2)cos(

!T=

+(2

)

,sin(

!T=

2)sin(

!T=







(75)

where

is white noise with covariance

=diag









(76)

This model was successfully used as a building block

of a multiple-model algorithm for aircraft tracking

application in an air defense system [77, 78].

The above model uses (65) for the turn rate

per se. Instead, it may be better to use (67). The

corresponding discrete-time model need be modified

accordingly.

1348 IEEE TRANSACTIONS ON AEROSPACE AND ELECTRONIC SYSTEMS VOL. 39, NO. 4 OCTOBER 2003

The discretized linearization (i.e., discretization

after linearization) alternative of this model can be

found in [73, 64], along with a comparison of its

performance with that of the linearized discretization

based on a theoretical error analysis

and Monte

Carlo simulations. It was concluded therein that

whenever possible linearized discretization is

preferable to discretized linearization. For the two

CT models with polar velocity, the former slightly

outperforms the latter. It was also claimed therein that

the CT model with polar velocity outperforms the CT

model with Cartesian velocity.

The use of the following variant of the above

CT model with polar velocity was reported in [79].

Let the state vector be

]



;thatis,

replace the turn rate

in the above model with the

normal (transversal) acceleration

. Then, it follows

immediately from (57)–(60) that the continuous-time

state-space model for the CT motion is given by

(5) with

(

)=[

cos

sin

,0,

,0]



discrete-time linear approximation of this model was

obtained based on a refined Euler-Cauchy scheme as

[79]

(

)) +

(77)

followed by the standard EKF linearization, where

is white noise, obtained by a backward difference

of (the derivative of) the continuous-time white

noise. Note that



(

). A set of

such unknown acceleration models was included

in a tracker for ATC in [79] to account for possible

horizontal motions.

C. Circular Motion Models

For a circular motion of a target, if its center were

known, the simplest model would be to represent the

circle in the polar coordinates and place the origin at

the circle center. In this coordinate system, the target

dynamic model is linear for

]



= diag[1,

]

+ diag[1,

]

(78)

where

and

were given by (14) and

is white

noise. The corresponding measurement equation

is pseudo-linear because the noise covariance is

actually state dependent, described in detail in a

subsequent part (see [15] for a preliminary version).

As a result, the Kalman filter is not optimal but

can be nonetheless implemented straightforwardly.

This

maneuver-centered

CT model was introduced

in [80]. While the idea underlying this model is

intuitively appealing, the inherent nonlinearity of

the problem is not avoided. It obviously relies on

an accurate determination of the center of the turn

Based on estimation of the Frobenius norm of the neglected terms

in the approximations.

in terms of the sensor coordinate system, which is

inherently a nonlinear problem. The following simple

geometrically oriented procedure of estimating the

center was proposed in [80]. Assume that each target

position measurements are points on the circle; replace

the chord between any two consecutive measurement

points with the straight line segment connecting them;

the center can then be determined from the (average)

intersection of the perpendicular bisectors of two or

more such straight line segments. An essentially the

same procedure was used in [81] for estimating the

center . Note that using the center estimates injects

additional nonlinearities into the system, which are

not accounted for in the above linear model.

D. Curvilinear Motion Model

This model, proposed in [82], is more general than

those considered so far in this section. It accounts

for possibly non-zero normal (cross-track) and

tangential (along-track) target maneuver accelerations

simultaneously. For the Cartesian state vector

[

]



, it follows from the standard equations

of curvilinear motion (57)–(60)

that this model in

continuous time is given by

(

))

(

) (79)

where

]



is the acceleration for the maneuver ,

was given by (11), and

(

)) =







(

)

(

)

(

)



(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)







(80)

Pretending the solution formula for the linear system

works for this actually nonlinear case, its discretized

version (by the standard discretization) in the form

(

)

(81)

is highly nonlinear because of its dependence on the

target state via matrix

(



)

(

))

d¿

(82)

and the integration involved in

(

)ishardto

evaluate exactly. It was shown in [82] that

(

) can

be found approximately to be, with

The heading angle

defined in [82] differs from the traditional

one, which is adopted here.

LI & JILKOV: SURVEY OF MANEUVERING TARGET TRACKING. PART I: DYNAMIC MODELS 1349

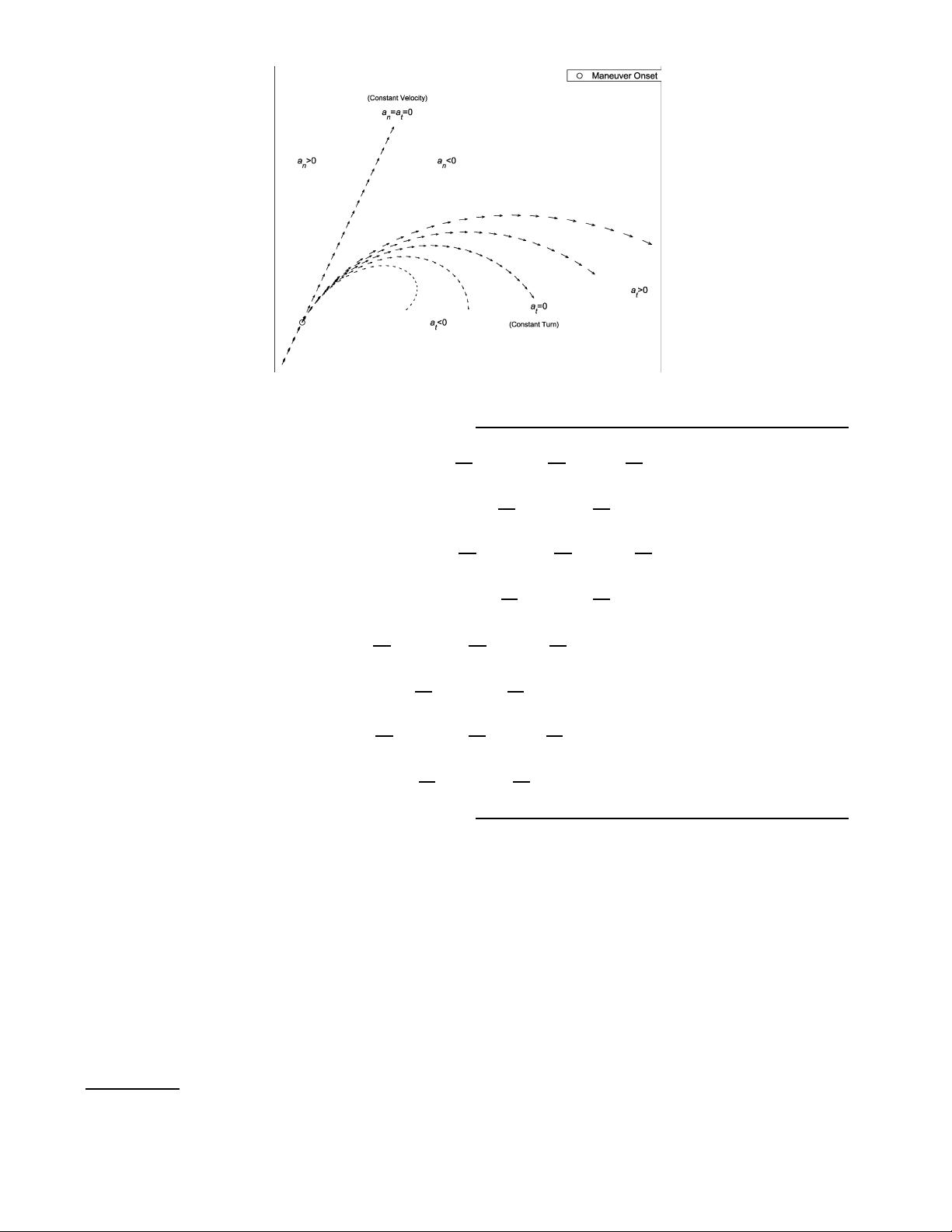
E. Ship Models

The maneuver models surveyed in this paper,

especially those for 2D horizontal motions and

all 3D models of the next section, are particularly

suitable for aircraft. These models were developed for

target tracking purposes. For other (e.g., navigation)

purposes, numerous, more precise dynamic models

can be found in the literature on vehicle dynamics

(see, e.g., [83–86]), which is beyond the scope of

this survey. These models, however, require better

knowledge about the vehicle than what is available

to a tracker. A fe w of these models have been adapted

to tracking applications, resulting in vehicle dynamics

based models. An example is those for aircraft based

on flight dynamics described in Section VID. Note,

however, that they are not really point-target models.

Likewise, a number of precise ship motion models

based on ship dynamics are available in the literature,

which depend on the particular ship’s form and

size. There exist also less precise but more generally

applicable models. The following model from [87] is

one in the latter class

sin(



) (86)

cos(



) (87)

(88)

K

(89)











(90)



[

q¯

] (91)

(92)









(93)

where model noise is not included for simplicity.

Here (



are ship position, heading,

(heading) turn rate, velocity vector turn rate,

drift angle, and control ruder angle deviation,

respectively;

(



)and

(0) are ship speeds

at turn rate



and



= 0 (i.e., at the onset of the turn),

respectively; the hydrodynamic constants

depend on ship geometry and size, in particular, ship

length

. The main feature of this model of a ship,

which is a sizable object, is revealed by (89) that

relates two turn rates and by (92) that relates two

speeds. The discretized version of this model with

Heading is the angle of the longitudinal axis and velocity heading

is the angle of the velocity vector . W e use either term if they

coincide or one does not exist (strictly speaking, a point target

without a shape has no heading). Turn rate is usually defined as the

heading change rate.

= 0 is given by [88, 89, 66]

sin

(94)

cos

(95)

[



(







)

¿e

] (96)





) (97)

(1 + 1



)



(98)

where



)

and



=v

The time constant

was set to zero in [88, 90],

resulting in a constant turn rate (i.e.,



to eliminate the dependence of the model on the

ship-specific hydrodynamic constants. However,

the ship length

was actually treated as known

therein. The unknown



was assumed to take on

one of the three possible values







with a

preset constant



, representing rectilinear, left-turn,

and right-turn motions, respectively, and the tracker

presented therein was based on a multiple-model

algorithm using these three models for



The above nonlinear model has been proposed for

ship tracking [88, 89, 66]. Other ship dynamic m odels

are available (see, e.g., [91, 33, 92]), some of which

appear simpler and more popular.

VI. 3D MOTION MODELS

Many of the 2D horizontal models reviewed

above have been considered for application to 3D

tracking of civilian aircraft in ATC systems. Such

targets maneuver mostly in a horizontal plane with

nearly constant speed and turn rate and have little

or limited vertical maneuver, usually performed not

at the time of a horizontal turn. Thus, the altitude

changes are most often modeled independently by a

(nearly) CV model or a random walk model along

direction, leading to an acceptable accuracy in

practice. Howe ver, when the task is to track agile

military aircraft, capable of performing “high-

”

turns in the 3D space (e.g., for tracking in air defense

systems) rather than just horizontally, decoupled

models may be inadequate. Many efforts have been

devoted to solving this problem, and more accurate

models have been developed, which are surveyed next.

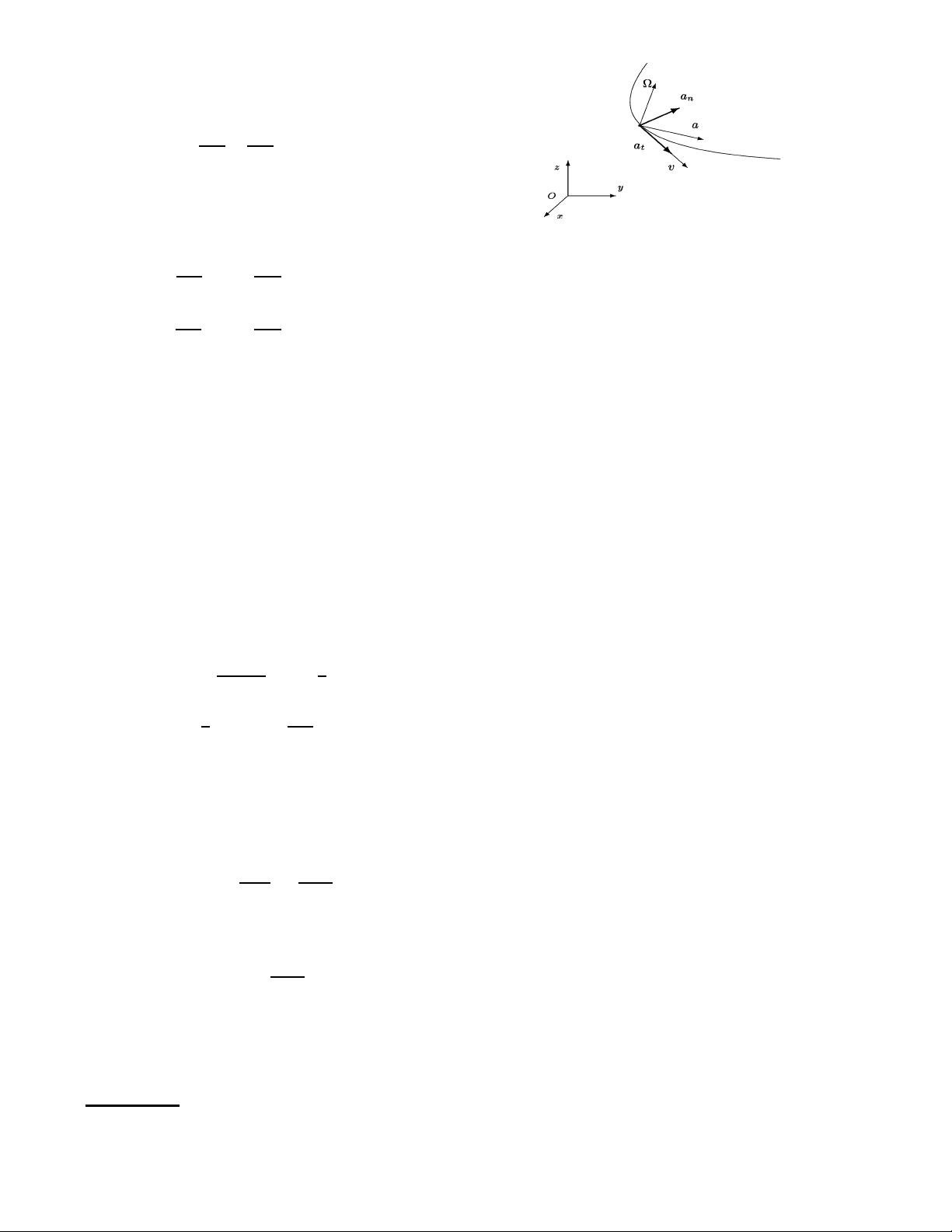
A. Basic Kinematic Relations

Let



be target position,

velocity, and acceleration, respectively, in the inertial

(Cartesian) frame

xyz

,where

is the target

center. Denote

»´³

as the target body frame.

The angular velocity vector of the target is defined

in the body frame as



) and in an arbitrary

frame (e.g., the inertial frame

) as [93, 86]



p»

q´

r³

with



(99)

LI & JILKOV: SURVEY OF MANEUVERING TARGET TRACKING. PART I: DYNAMIC MODELS 1351

where

are expressed in that arbitrary frame.

The fundamental relation of kinematics (FRK) [86,

94] states that for any time-varying vector

(

)we

have





(100)

where

and

are

expressed in the inertial frame

and the body frame

, respectively, and



is the

angular velocity vector of

with respect to

.This

relation holds true in all frames. For example,













(101)













(102)

where superscripts

and

denote quantities

expressed in

and

frames, respectively. In the

sequel, for simplicity we drop superscript

and

write

and

for

=dt

and

=dt

, respectively.

However, we maintain the less compact notations

=dt

and

=dt

, rather than the misleading

and

because the latter are likely to be incorrectly

interpreted as (

=dt

)

and (

=dt

)

, respecti vely.

Note that since the target body frame

rotates as the

target does, we have



,where



is the angular

velocity vector of the target in the inertial frame

In what follows, we consider only the important

case

where the »-axis of the body frame is aligned with

the velocity vector

,thatis,

,where

the target speed. Then by the Poisson’s formula [93]





,wehave







that is,











(103)

meaning that the total acceleration is the vector sum

of a linear acceleration (

)

and an acceleration





responsible solely for turning. This relation also

follows directly from FRK (100) with

and

. Further, it follows from (103) by straightforward

calculus

that







(104)

It turns out that (103) and (104) are equivalent.

It is clear from (104) that the angular velocity is

given by





(105)

if and only if





=0,thatis,



.Itfollows

from (105) that



and that

and

are in a plane

(known as the maneuver plane) orthogonal to



and thus the motion is planar, but not necessarily

horizontal, if



has a constant direction. Note that

v  a = v 

v = v  (



 v)=(v  v)



 (



 v)v =



 (



 v)v.

Fig. 8. Geometry of a 3D orthogonal-velocity motion.

this is the case even if





= 0 (i.e., turn rate is not

constant) provided



has a constant direction.

Equation (105) plays a central role in most 3D

kinematic models. Virtually all models in the literature

(e.g., [95, 10, 96, 97, 70, 6, 98, 1, 99]) presume

explicitly or implicitly that (105) holds. As shown

above, a necessary and suf ficient condition for its

validity is the orthogonality between the linear and

angular velocity vectors. In this sense, models that

obey (105) are orthogonal-velocity models, although

they are widely referred to as “

coordinated turn

”

models, which is actually a misnomer. The geometry

of these models is illustrated in Fig. 8.

The FRK (100), (103), and (104) (or (105)) are

the key to understand various 3D maneuver models

proposed in the literature.

Since the target tracking community is more

familiar with the matrix language than the vector

analysis and we are more concerned with state-space

models, in the sequel we use the following

relationship repeatedly. Let



]



and

]



.Then













































(106)

B. Constant-Turn Models

3D Constant-Turn Models

: It is clear from

(103) that a constant speed (i.e.,

= 0) motion

corresponds to



= 0 (i.e.,

) and is described

equivalently by





(107)

Since



is unknown in general, one of the simplest

possible way is to augment the state vector by its

components



in the inertial frame, to be

estimated. That is, let



]



Then (107) becomes

















































































(108)

1352 IEEE TRANSACTIONS ON AEROSPACE AND ELECTRONIC SYSTEMS VOL. 39, NO. 4 OCTOBER 2003

剩余191页未读，继续阅读

shg736940118

粉丝: 0
资源: 7

空中目标跟踪技术综述：动态模型分析

关于追踪模型的论文

unity3D鼠标空中自由漫游

基于空中目标识别的特征提取与选择 (2014年)

红外弱小目标检测与跟踪问题

红外多目标检测与跟踪算法研究

无人机数据-目标检测-多目标跟踪-空中小目标检测-drone_ROI_high_416.zip

运动场景中目标检测与跟踪技术研究.pptx

运动场景中目标检测与跟踪技术研究课程.pptx

运动视频场景中目标检测与跟踪技术应用研究.pptx

一种空中目标航迹自适应跟踪算法

最新资源