最短路算法详解与应用实践

"余远铭《最短路算法及其应用》" 本文由广东北江中学的余远铭撰写，深入探讨了最短路问题在图论中的重要地位以及其广泛的实际应用。最短路问题不仅是许多高级算法的基础，而且在众多看似无关的问题中都能找到它的身影。文章详细阐述了最短路问题的基本概念，包括定义、简单变体、负权边的情况以及松弛技术。接着，文中介绍了三种常用的最短路算法：Dijkstra算法、Bellman-Ford算法和SPFA算法，分别分析了它们的工作原理和适用场景。 在应用举例部分，作者通过具体的例题展示了最短路算法在货币兑换、双调路径、Layout优化和网络提速等问题上的应用。这些实例帮助读者理解如何建立模型，运用所学算法解决问题，并提供了思考和证明过程。 文章的最后，作者进行了总结，回顾了最短路问题的核心内容，强调了解决这类问题的重要性，以及理论知识在实际问题解决中的价值。对于想要深入了解最短路算法及其应用的读者，这篇文章提供了一个全面而实用的指南。 最短路问题的基本概念包括： 1. 定义：在有向加权图中，从一个节点到另一个节点的路径的权值是路径上所有边权重的总和，最短路径是指具有最小权值的路径。 2. 简单变体：包括单目标最短路径问题（所有节点到指定节点的最短路径）和单对结点间的最短路径问题（特定两个节点间的最短路径）。 3. 负权边：如果图中存在负权边，某些最短路径算法需要特殊处理，因为负权边可能导致最短路径不是简单的路径。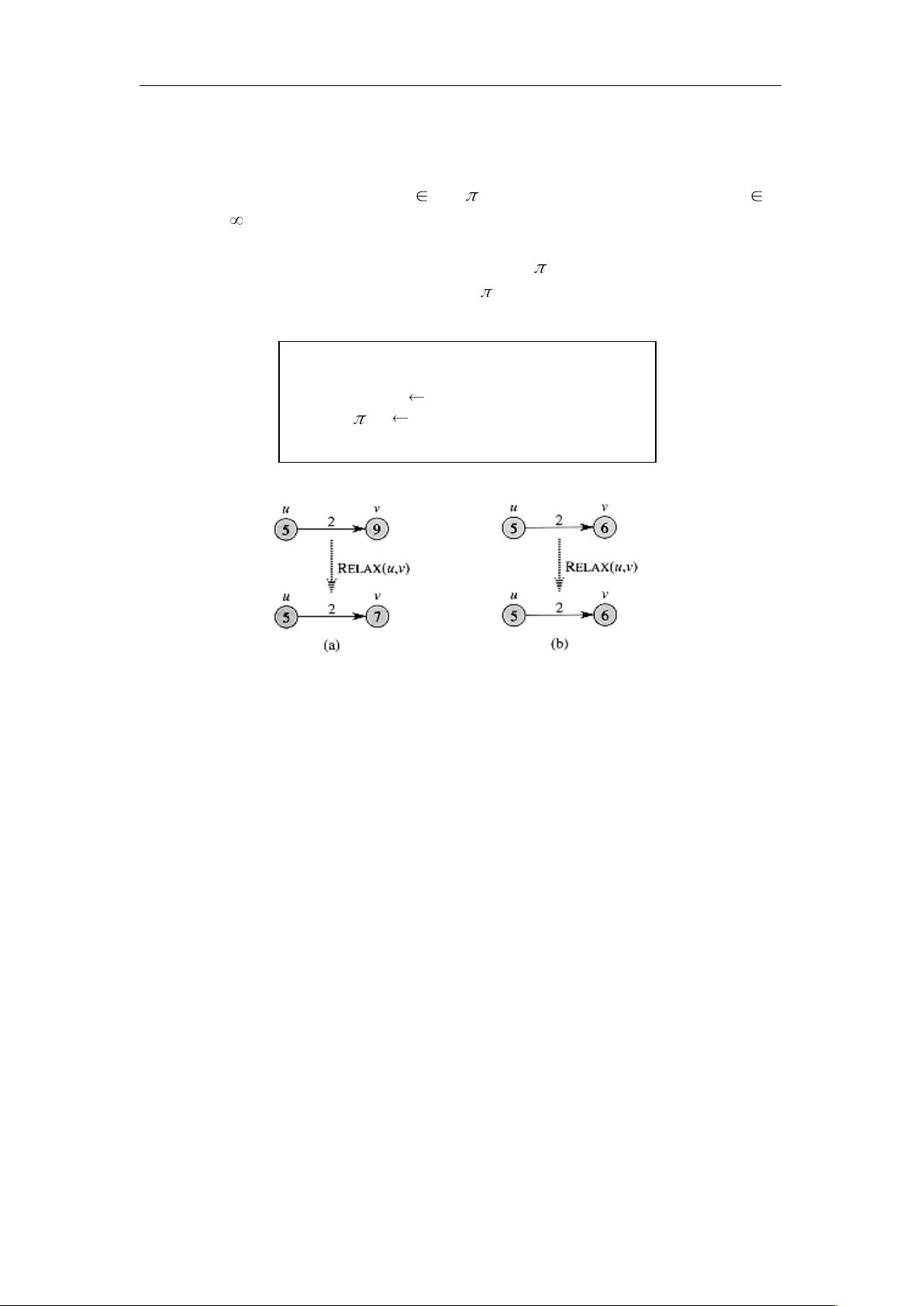 4. 松弛技术：用于更新路径信息，逐步优化最短路径估计。 常用的最短路算法包括： 1. Dijkstra算法：适用于没有负权边的图，能有效找到单源最短路径。 2. Bellman-Ford算法：能够处理包含负权边的图，但时间复杂度相对较高。 3. SPFA（Shortest Path Faster Algorithm）算法：一种基于队列的数据结构优化的Bellman-Ford算法，通常在实践中表现较好，但可能不是最坏情况下的最优算法。 通过对这些问题和算法的详细探讨，余远铭的文章为读者提供了一套完整的最短路问题学习框架，有助于提高读者在图论和算法设计方面的能力。