优化算法解析：梯度下降法与牛顿法

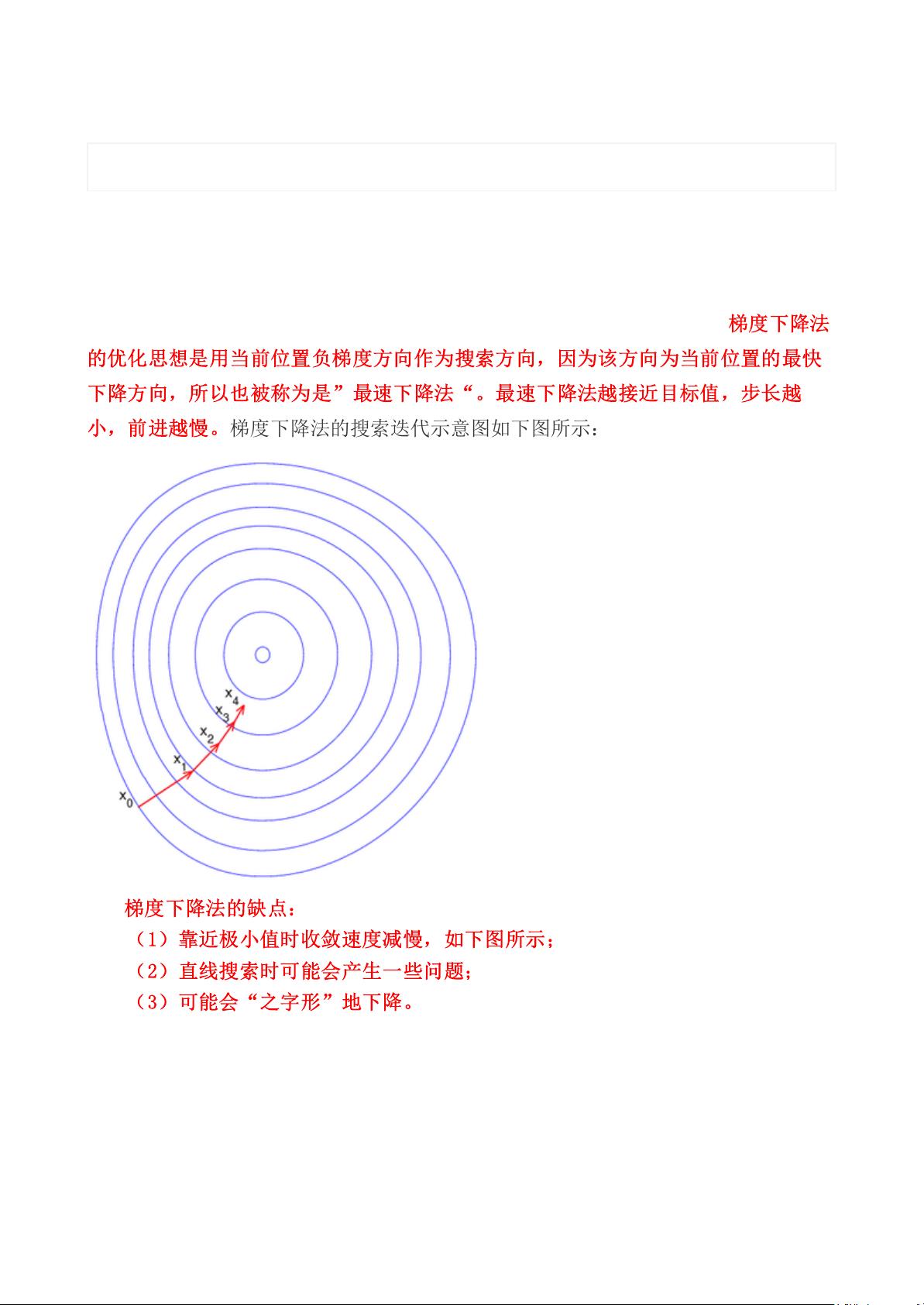
"优化算法在IT领域中扮演着重要的角色，特别是在机器学习和数据分析中用于找到最佳模型参数。本文主要介绍了几种常见的最优化算法。 1. 梯度下降法 梯度下降法是最基础也是最常用的优化算法之一，主要用于求解损失函数最小化的参数。它通过沿着损失函数梯度的负方向进行迭代更新，逐步逼近极小值。优点是实现简单，适合大规模问题。然而，梯度下降法存在几个缺点： - 收敛速度在接近极小值时变慢，导致迭代次数增多。 - 直线搜索可能存在问题，如步长选取不当可能导致震荡或缓慢收敛。 - 可能出现“之字形”下降路径，导致非平稳收敛。 随机梯度下降（SGD）是梯度下降法的一个变体，每次迭代仅使用一个样本来更新参数，这大大减少了计算量，尤其在大数据集上表现优秀。尽管SGD的每一次迭代可能不朝着全局最优方向，但总体趋势是朝向全局最优解，因此在处理大规模样本时效率更高。 2. 批量梯度下降（BGD） 与SGD相反，BGD使用所有训练样本来计算梯度，因此它找到的解是最优解，即风险函数最小的参数。然而，由于需要处理所有样本，对于大规模数据集，计算效率较低。 3. 牛顿法 牛顿法是一种基于二阶导数的优化算法，通过构造泰勒展开式来寻找函数的零点。其特点是收敛速度快，通常具有平方收敛的特性。牛顿法的迭代公式为： \( x_{k+1} = x_k - \frac{f'(x_k)}{f''(x_k)} \) 其中，\( f'(x_k) \) 和 \( f''(x_k) \) 分别是函数在 \( x_k \) 处的一阶和二阶导数。牛顿法需要计算二阶导数（Hessian矩阵），在高维问题中计算成本较高，且若Hessian矩阵不可逆，可能导致算法不稳定。 4. 拟牛顿法 为了解决牛顿法中计算二阶导数的困难，人们发展出了拟牛顿法，如BFGS和L-BFGS算法。这些方法通过近似Hessian矩阵来模拟牛顿法的特性，同时避免直接计算Hessian，降低了计算复杂性。 5. 共轭梯度法 共轭梯度法是解决大型线性系统的一种有效方法，特别是对于对称正定矩阵。它不需要存储和计算Hessian矩阵，只需要一阶导数信息，且在有限的迭代次数内达到全局最优解。 不同的优化算法有各自的适用场景和优缺点。在实际应用中，需根据问题的规模、计算资源以及对精度的要求来选择合适的算法。例如，对于小规模问题，牛顿法可能是首选；而大规模数据集通常更适合使用SGD或其变种。在实际操作中，还可以结合其他技术，如学习率调整、早停策略等，来进一步提升优化效果。"