利用相关分析法识别脉冲响应：实验报告

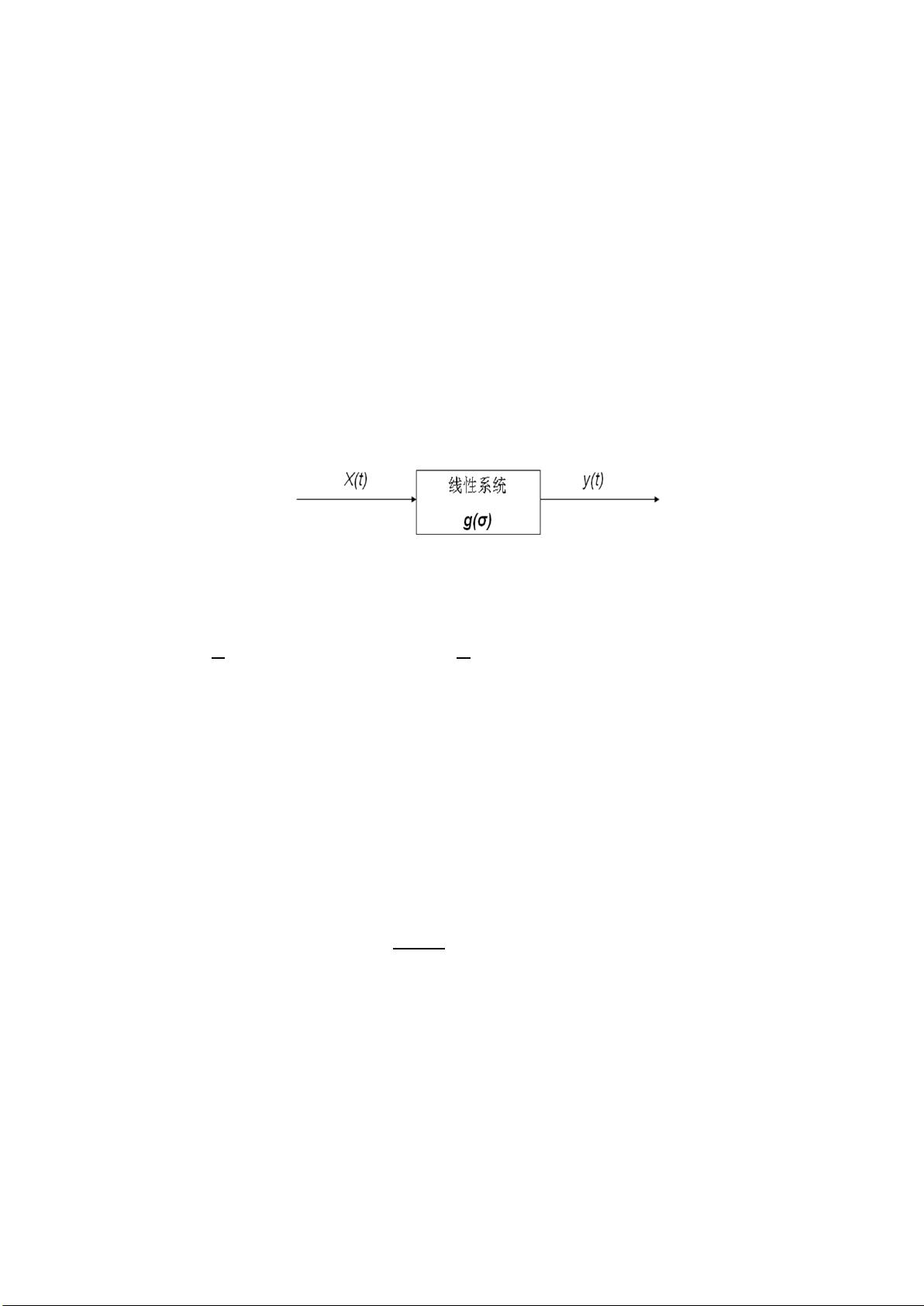
"哈尔滨工业大学（深圳）《系统建模与仿真》课程实验报告，利用相关分析法辨识脉冲响应的原理和方法。" 本文主要介绍了一种利用相关分析法来辨识脉冲传递函数的方法，该方法适用于单入单出线性定常系统的动态特性分析。脉冲传递函数是描述系统动态行为的关键参数，它反映了系统对输入信号的瞬时响应。在实验中，通过记录输入信号x(t)和输出信号y(t)的值，并计算它们的互相关函数，可以求得脉冲响应函数g(τ)。 实验目的旨在让参与者掌握相关分析法的原理和应用，以便于识别系统的脉冲响应。实验内容涉及一个包含过程输入u(k)，输出z(k)以及噪声v(k)的系统模型。系统的传递函数G(s)由比例系数K，时间常数Ts1和Ts2构成。输入驱动使用M序列，这是一种伪随机二进制序列，具有良好的自相关性和低的互相关性，适合用于辨识系统的特性。输出信号受到白噪声v(k)的影响，v(k)服从正态分布，具有零均值和一定的方差。 实验要求包括设计仿真方案，模拟过程传递函数，获取输出数据，并使用M序列作为输入信号，白噪声作为干扰。通过计算互相关函数，可以得到不同λ值下的脉冲响应估计值g^(k)，脉冲响应理论值g0(k)，以及脉冲响应估计误差g~(k)。当k趋近于无穷大时，期望误差g~(k)接近于零。此外，实验还需要计算信噪比并绘制实验流程图，所有这些操作都需要通过MATLAB编程实现。 实验原理部分指出，一个系统的动态特性可以用脉冲响应函数g(τ)表示，它是系统在单位阶跃输入下的输出随时间的变化。根据维纳-霍夫积分方程，可以通过计算输入和输出的互相关函数，然后取极限来求解脉冲响应。具体公式为： \[ y(t) = \int_{-\infty}^{t} g(\tau)x(t - \tau)d\tau \] 这里，y(t)是系统输出，x(t)是系统输入，g(τ)是脉冲响应函数。在实际操作中，由于数据的有限性，通常使用有限时间内的数据来近似计算互相关函数，从而得到脉冲响应的估计。 相关分析法是一种实用的系统辨识技术，它通过分析输入和输出信号的相关性来估计系统的动态特性。在系统建模与仿真领域，这种技术被广泛应用于各种控制系统的设计和分析。通过MATLAB编程，可以有效地实现这一过程，为理解和优化系统性能提供重要依据。