子模函数学习：凸优化方法

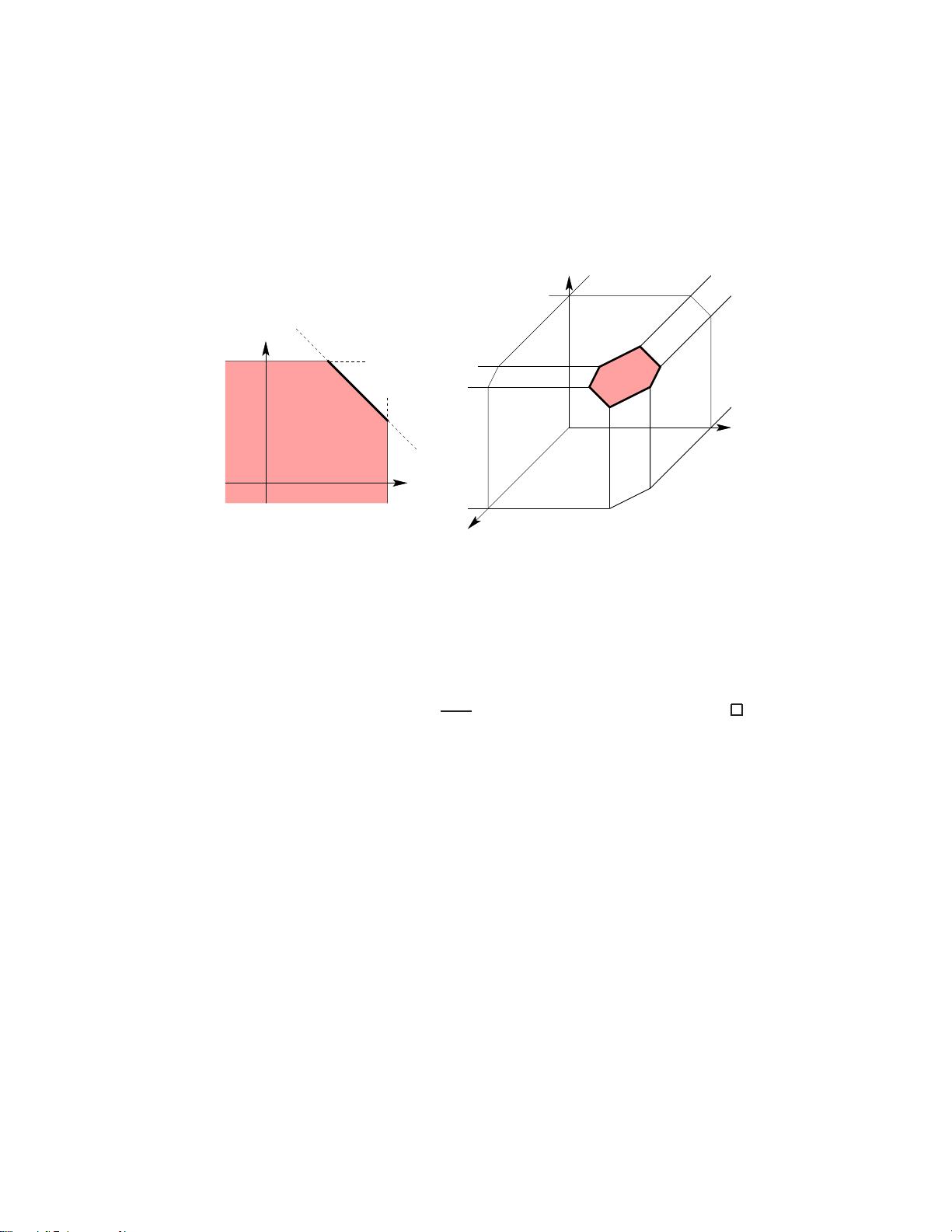
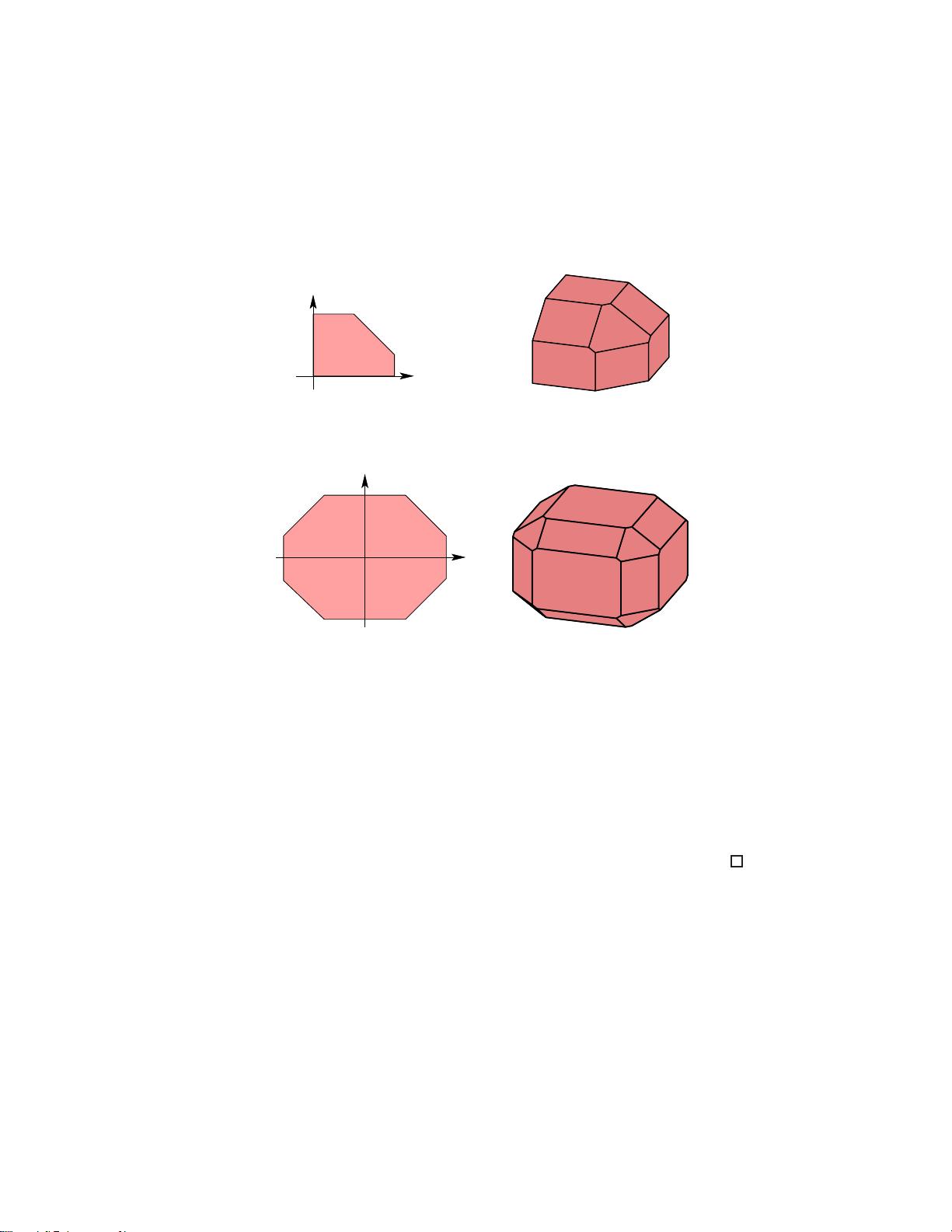
"Learning with Submodular Functions - A Convex Optimization Perspective" 本文主要探讨了使用子模函数进行学习的理论和方法，从凸优化的角度出发，深入解析子模函数的特性及其在机器学习中的应用。作者 Francis Bach 是来自法国巴黎 INRIA-Ecole Normale Supérieure 的专家。 1. 引言 文章首先介绍了子模函数学习的基本概念，指出这种学习方法在处理优化问题时的高效性和广泛适用性，特别是在面对非线性和复杂数据结构时的优势。 2. 定义 子模函数的定义被详细阐述，包括等价定义，以及与之相关的多面体（polyhedra）的概念。子模函数的性质使得它们在保持效率的同时，能够捕获数据中的复杂依赖关系。 2.1 等价定义：子模函数的多个定义被比较，强调其单调性和局部减少的特性。 2.2 相关多面体：这些多面体是子模函数的几何表示，对于理解和解决与子模函数相关的优化问题至关重要。 2.3 多形体（Polymatroids）：这是非递减子模函数的特定类型，特别适用于描述资源分配等问题。 3. Lovász 扩展 Lovász 扩展是子模函数理论的核心工具，它将子模函数扩展到连续域，从而允许使用连续优化方法处理离散问题。 3.1 定义：阐述了 Lovász 扩展的数学形式，它是将子模函数与一个凸函数关联起来的关键。 3.2 贪心算法：在子模函数优化中，贪心策略通常能获得近似最优解，这与 Lovász 扩展有关。 3.3 子模函数与凸性的联系：讨论了子模函数的某些特性如何与凸性相联系，这对于构建有效的优化算法至关重要。 4. 相关多面体的性质 这部分深入研究了与子模函数相关的多面体的几何和代数特性，包括支撑函数、面结构和对称子模多面体。 5. 子模惩罚的凸松弛 这部分探讨了如何利用凸松弛技术来处理子模函数的优化问题，特别是对集合函数的凸和凹闭包的研究，以及结构化稀疏性和组合惩罚的凸松弛。 5.1 凸和凹闭包：这是构造有效优化算法的基础，通过这些闭包可以找到子模函数的可操作近似。 5.2 结构化稀疏性：子模函数在处理稀疏优化问题时特别有用，能够选择最重要的元素或特征。 5.3 组合惩罚的凸松弛：通过放松原始的非凸组合约束，可以找到接近最优的解决方案。 5.4 ℓ_q 软化：这是一种特定的松弛技术，用于处理子模惩罚的非凸性。 5.5 形状水平集：这与子模函数的值域相关，有助于理解优化问题的解决方案空间。 6. 子模性的例子和应用 最后，文章列举了若干子模函数在实际问题中的应用，如基于基数的函数，这些函数在压缩感知、图像分割、推荐系统等领域有广泛的应用。 本文提供了一个全面的视角，展示了子模函数在机器学习和凸优化中的强大能力，为研究者和实践者提供了理解和利用这些函数的坚实基础。