数字电路复习指南：从数制转换到逻辑函数详解

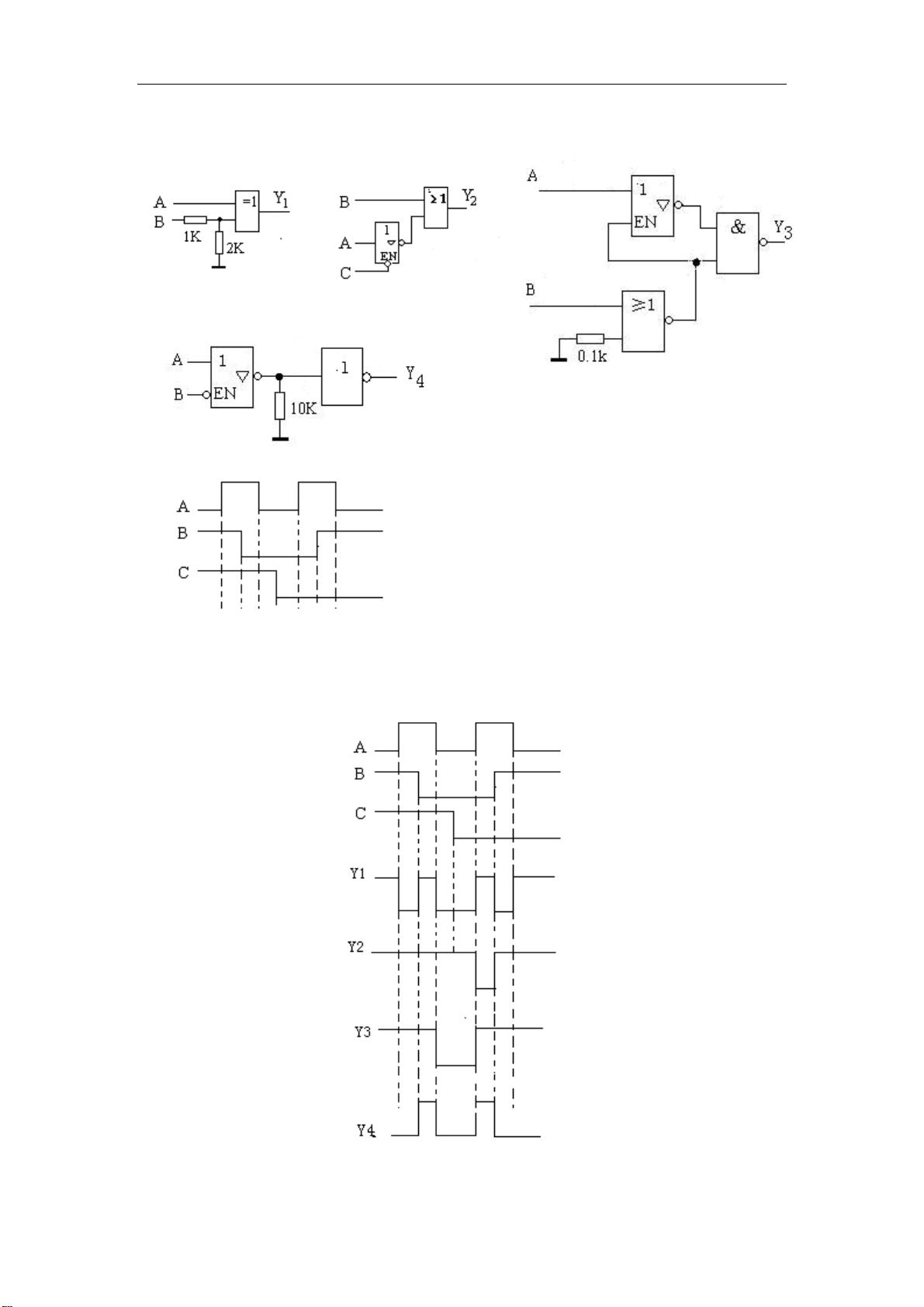
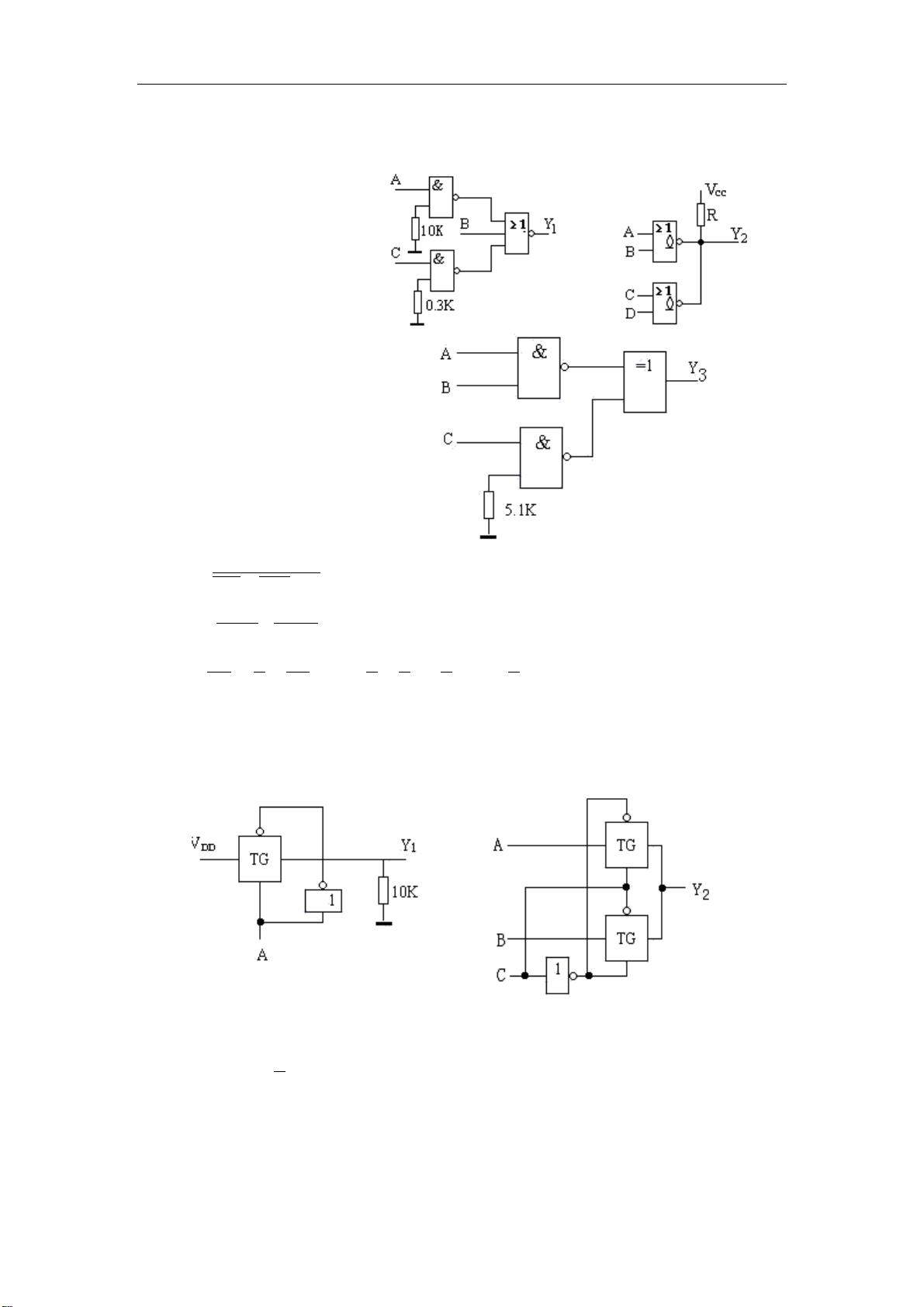
该文档是一份针对大学考试的数字电路复习指南，包含了丰富的知识点和实例。以下是主要内容的详细解析： 1. 第一章：逻辑代数基础 - 数制及转换：这部分强调了不同数制（如二进制、八进制和十六进制）之间的转换技巧，例如提供了一些具体的转换示例，如(46.125)10到(2E.2)16。 - 码制与表示：介绍了BCD码（Binary-Coded Decimal），即四位一组的二进制数来表示十进制数，如将(10110010110)8421码转换为十进制数(596)10。 - 原码、反码和补码：讲解了如何表示正数和负数的原码、反码和补码，例如(-35)10在不同数制下的表示形式。 2. 逻辑函数表示与化简 - 逻辑函数的表示方法：包括逻辑表达式的表示，如用AND、OR、NOT等基本逻辑运算符构建逻辑函数。 - 最小项之和的标准形式：学习如何将逻辑函数转换为标准的最小项之和（Sum-of-Minimum Terms, SOP）形式。 - 逻辑函数化简：重点介绍两种化简方法，公式法（如Karnaugh Map, K-map）和卡诺图法，用于简化逻辑电路的设计。 3. 逻辑代数基本定理： - 定义和应用：这部分介绍了逻辑代数的三个基本定理，如德摩根定律、分配律和结合律，这些都是理解和设计逻辑电路的基础。 4. 例题与练习： - 提供了一系列实际问题，如数制转换、数值的原反补码计算、BCD码转十进制以及逻辑函数的求解，旨在帮助学生巩固理论知识并提升实践能力。 通过这份复习资料，学生可以系统地复习数字电路中的基础知识，包括数制转换、逻辑运算、编码规则以及逻辑函数的分析与简化。这对于准备相关考试的学生来说，是理解和掌握数字电路设计的关键参考资料。