理解Logistic回归分析及其应用

"该资源是一份关于统计学中logistic回归分析的PPT课件，主要探讨了在计算机科学领域，尤其是数据分析时如何运用logistic回归来处理分类问题。" 在统计学和计算机科学中，logistic回归是一种广泛应用的分析方法，特别是在处理分类数据时。它属于概率型非线性回归模型，主要用于研究离散型因变量（通常是二分类，如发生或不发生，是或否等）与一个或多个自变量（可以是连续、等级或分类变量）之间的关系。与传统的多元线性回归不同，logistic回归能够处理因变量不是连续性随机变量的情况。 在医学研究中，logistic回归经常被用来探究某个疾病的发生与一系列因素（如高血压史、高血脂史、吸烟等）之间的关联。例如，研究者可能想知道暴露于特定风险因素（如高血压、高血脂和吸烟）是否会增加冠心病的发生概率。而由于疾病的发生通常是非黑即白的二元结果（发生或不发生），不适合用线性回归模型，因此引入了logistic回归。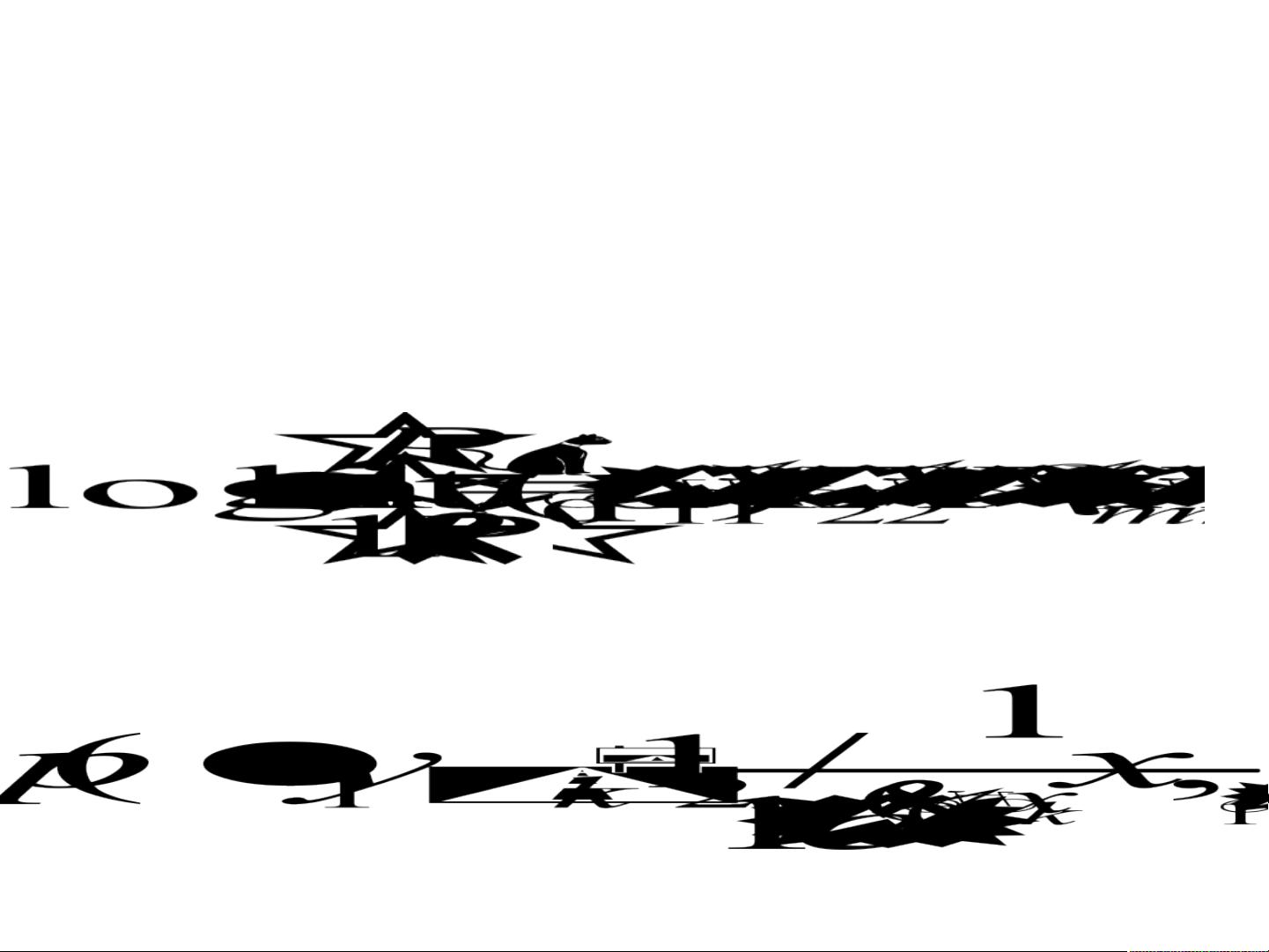 logistic回归的核心在于构建一个logistic函数，也称为逻辑函数，形式为 P = 1 / (1 + e^(-z))，其中z通常表示自变量的线性组合。这种函数的输出值P始终在0到1之间，代表了事件发生的概率。对于只有一个自变量的简单logistic回归模型，公式为 P = 1 / (1 + e^-(β0 + β1*x))，其中β0和β1是待估计的参数，β0代表截距，β1表示自变量x对因变量的影响。 logistic回归模型通过最大似然估计法进行参数估计，目的是找到一组参数，使得所有观察数据出现的概率最大化。模型的解释性很强，可以得出各个自变量对因变量的影响大小以及方向。比如，如果β1为正，那么自变量x每增加一个单位，事件发生的概率将增加e^β1倍。 在实际应用中，logistic回归可以进行模型拟合优度检验、显著性检验和预测。它不仅可以用于单因素分析，还可以进行多因素分析，以同时考虑多个影响因素。此外，logistic回归还能计算出预测变量组合下事件发生的累积概率，以及计算优势比，这在医学研究和公共卫生决策中具有重要意义。 logistic回归分析是统计学中处理分类问题的强大工具，它在计算机科学、医学研究、社会科学等多个领域都有广泛的应用。通过学习和掌握logistic回归，我们可以更好地理解和预测离散型结果与连续或分类变量之间的复杂关系。