Matlab实现基2-DIT FFT算法详解与效率提升

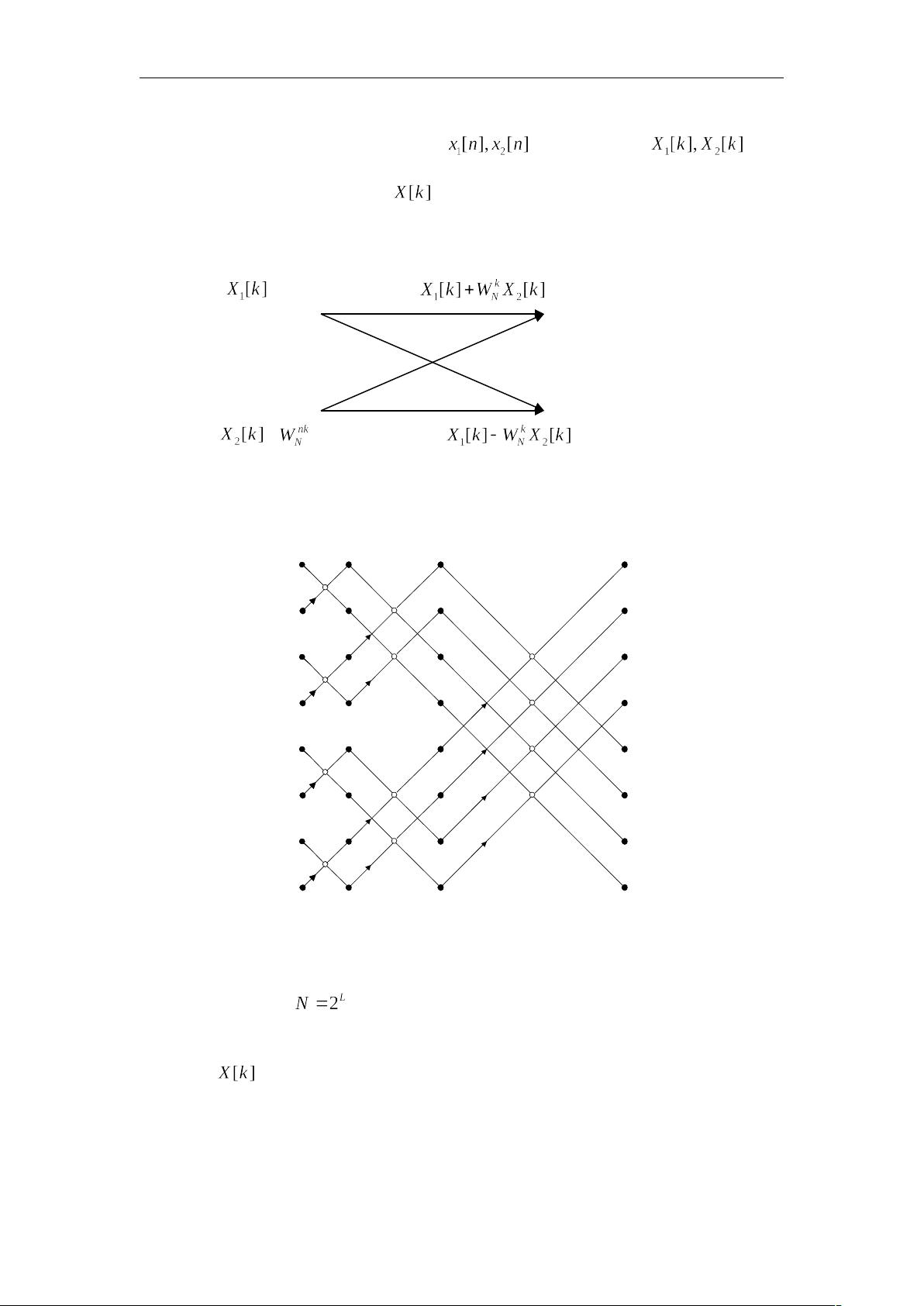
实验2是在Matlab中实现基2-DIT(按时间抽取)快速傅立叶变换(FFT)的详细教程。该实验针对的是电子科技大学数字信号处理实验室的课程任务，旨在让学生理解并掌握FFT算法在实际工程中的高效计算方法。 FFT（Fast Fourier Transform）算法的核心思想是减少离散傅立叶变换(DFT)的计算复杂度。DFT原本对于N点序列需要进行大量的复数乘法和加法操作，但直接计算成本高昂，特别是当N值较大时。FFT利用了分治策略，将大问题分解为小问题，逐步降低计算量。 在基2-DIT FFT中，关键步骤如下： 1. **DFT的定义**：对于长度为N的离散序列，其DFT可以通过公式[pic]来计算，其中[k]是频域的索引，n是时域的索引。旋转因子[r]简化了计算过程。 2. **直接计算DFT的问题与FFT基本思想**：常规的DFT计算复杂度是O(N^2)，这在处理大数据集时效率低下。FFT通过递归地将序列分为长度减半的子序列，然后合并它们的DFT，将计算复杂度降为O(N log N)。例如，对于偶数N，可以将计算量减半，只需计算两个(N/2)点DFT，重复此过程直到达到最小规模。 3. **基2按时间抽取(DIT)算法**：假设序列长度L可通过补零调整为2的幂，首先根据n的奇偶性将序列分为两部分。接着，对偶数点和奇数点分别进行DFT计算，然后通过旋转因子的性质将这两个DFT值组合起来。然而，这仅给出了前半部分的结果，还需利用旋转因子的周期性来获取后半部分的DFT值。 在Matlab中实现基2-DIT FFT时，学生会学习如何编写代码来执行这种分治策略，包括创建子序列、应用DFT函数、以及合并结果。此外，还会涉及如何优化代码以提高计算性能，并理解算法的时间复杂性和内存需求。 通过这个实验，学生不仅能够深入理解FFT的工作原理，还能提升编程技能，将理论知识应用到实际问题中，这对于在IT领域进一步研究和开发具有重要意义。