复杂网络中重叠和层次社区结构检测

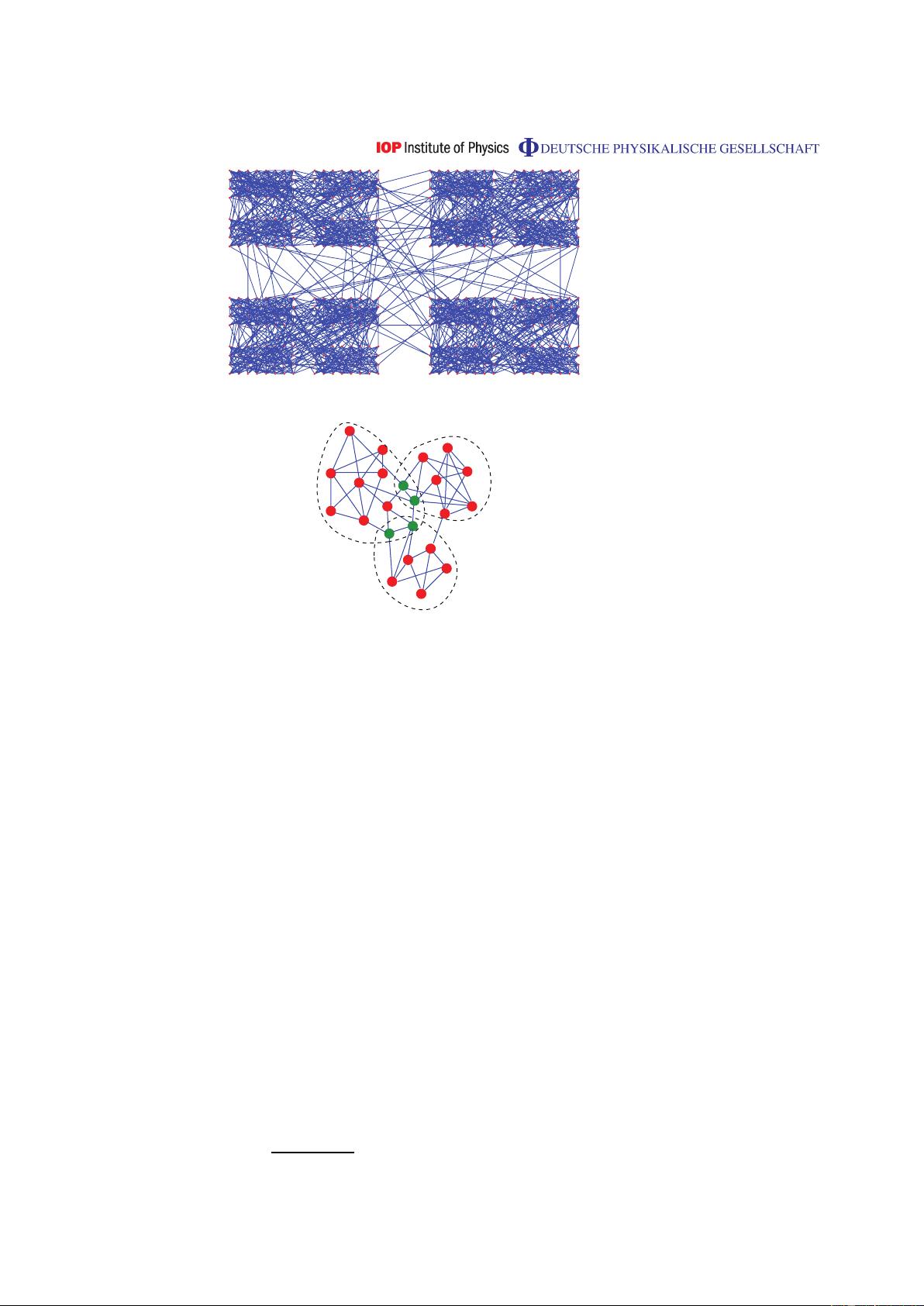
"LFM算法：检测复杂网络中的重叠和层次化社区结构" LFM算法，全称为Label Propagation for Multilayer Networks，是一种用于发现复杂网络中重叠和层次化社区结构的方法。该算法由Andrea Lancichinetti、Santo Fortunato和János Kertész在2009年的《新物理杂志》(New Journal of Physics)上发表。此算法的主要贡献在于，它能够处理那些节点可以同时属于多个社区，即存在重叠的网络，并且还能揭示网络中可能存在的层次结构。 在传统的社区发现算法中，通常假设每个节点只属于一个社区，但现实世界中的许多网络，如社会网络、科研合作网络或互联网，往往具有节点多重归属的特性。LFM算法正是针对这一问题提出的解决方案，它通过节点标签的传播过程来识别这些重叠社区。 LFM算法的工作原理大致如下： 1. 初始化：每个节点被赋予一个唯一的标签，这些标签可以被视为初始的社区划分。 2. 标签传播：在每一轮迭代中，每个节点会将其当前标签更改为与其相邻节点中最常出现的标签。 3. 平衡：当网络中没有标签发生变化时，算法达到平衡状态，此时的标签分配表示了网络的社区结构。 4. 重复和优化：这个过程可以多次进行，以找到更稳定的社区结构。在某些情况下，可能会通过引入额外的规则或约束来优化结果，例如限制社区的大小或数量。 LFM算法的创新之处还在于其对层次结构的识别。在某些网络中，社区之间可能存在嵌套或层级关系，即一部分社区可能是其他社区的子集。LFM通过分析不同迭代步长下的社区结构变化，能够揭示这种层次结构。 此外，LFM算法还考虑了网络的多层性质。在网络的不同层面上，节点的社区归属可能不同，LFM能够适应这种多维度的社区结构，为每一层提供独立的社区划分。 LFM算法的实用性和有效性已经在各种实际网络数据集上得到了验证，包括社会网络、科学合作网络和生物网络等。通过LFM，研究人员可以更好地理解和解析复杂网络的组织结构，从而深入洞察网络中隐藏的模式和动态。 尽管LFM算法在处理重叠社区和层次结构方面表现出色，但也有一些局限性，例如对于大规模网络的计算效率问题，以及在噪声和不完整数据中可能的稳定性问题。然而，LFM为后续研究提供了基础，推动了社区发现领域的进一步发展，促进了更多高效且适应性强的算法的诞生。