图和网络的关联矩阵：电路网络的数学模型

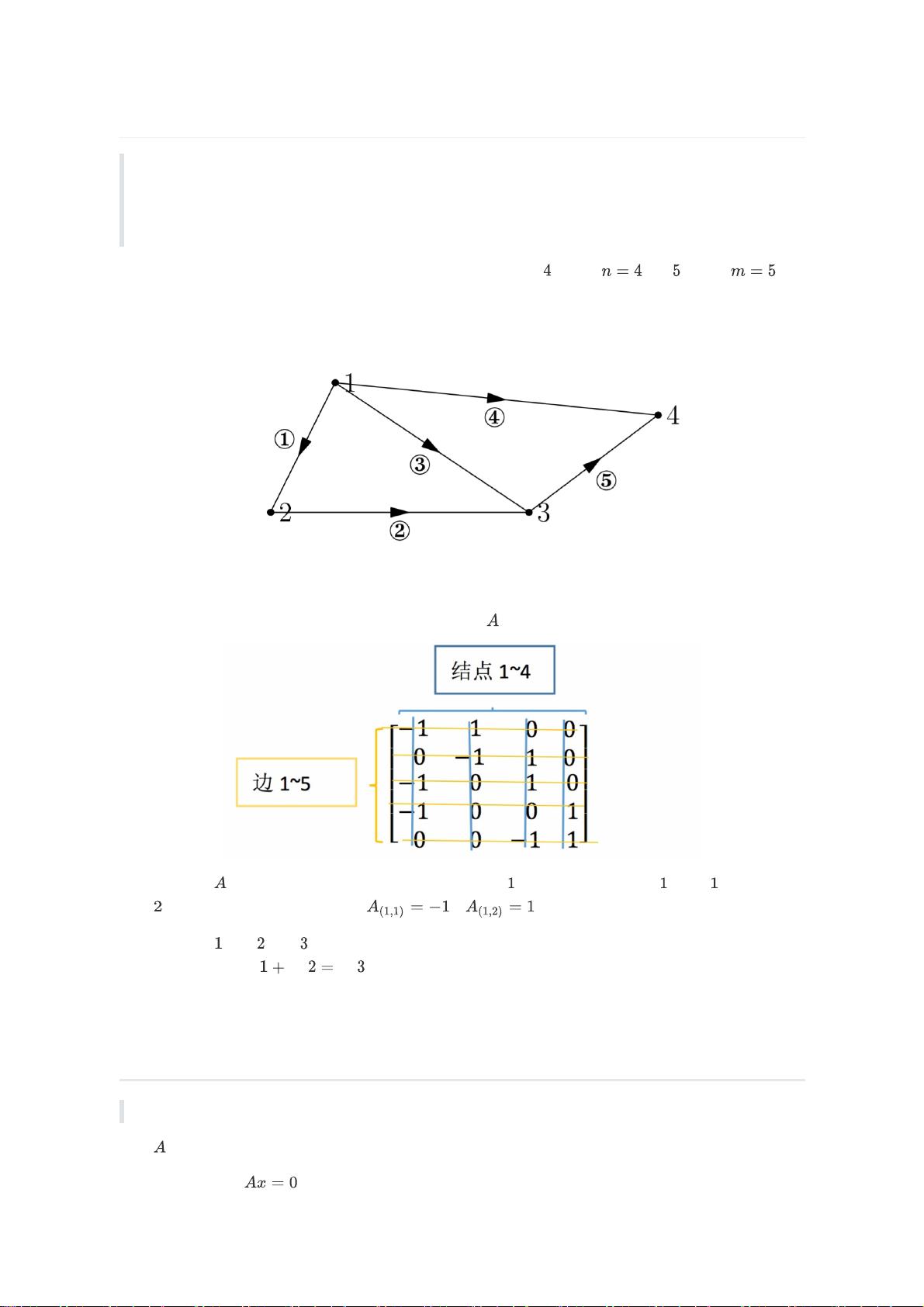
"线性代数在图和网络分析中的应用" 在第12课中，我们探讨了如何利用线性代数来理解图和网络，尤其是电路网络。图是离散数学中的一个重要概念，它能建模现实世界中的各种结构，如电路、液压系统或建筑结构。在本课程中，我们特别关注电路网络，这里的图由节点（或顶点）和边组成，边代表电流流动的路径。 关联矩阵是表示图的一种有效方式，它将图的边映射为矩阵的行，节点映射为列。对于电路网络，关联矩阵的每一行对应一条边，每行的非零元素表示起点和终点节点，且符号（正或负）指示电流的方向。例如，如果第一行的某元素为正，表示从某个节点出发；为负，则表示到另一个节点。矩阵的第一行描述了电路网络中特定边的起点和终点。 进一步分析关联矩阵，我们可以发现回路（环路）的特性。在电路中，如果多条边形成一个闭合路径，即回路，那么这些边在矩阵中对应的行就会是线性相关的。这是因为回路内部的电流总和为零，反映在线性代数中就是行向量组的线性相关性。 关联矩阵通常是非常稀疏的，因为它大部分元素都是零，仅有的非零元素记录了边的信息。例如，如果一个网络有n个节点和m条边，关联矩阵将是一个m×n的矩阵，其中每行只有两个非零元素，分别对应起点和终点。 接下来，我们探讨矩阵的主要问题。首先是零空间，它对应于矩阵方程Ax=0的解。对于电路网络，如果将零空间的解视为节点的电势，那么解表示所有节点电势相等的状态，即没有电势差。这意味着没有电流流过任何边，符合物理中的电势平衡条件。 接着是左零空间，即解方程xTA=0的问题。在这个上下文中，x表示各边上的电流。左零空间的解意味着在某种条件下，即使所有节点的电势固定，仍能找到一组电流值使得它们满足欧姆定律，即电流等于电势差除以电阻。这进一步巩固了线性代数在电路分析中的应用，它允许我们用数学工具来理解和预测电路的行为。 线性代数的工具，如关联矩阵，使我们能够对复杂的图和网络结构进行精确的数学建模。通过分析这些矩阵，我们可以推导出像欧姆定律和基尔霍夫定律这样的基本电路原理，以及它们与图论中的欧拉公式之间的关系。这种理论不仅适用于电路分析，还可以应用于其他具有类似网络结构的领域，如流体动力学或结构工程。通过深入理解和运用这些概念，我们可以更好地理解和解决实际问题。